陕西省西安市新城区2022-2023学年九年级上学期第一次月考数学试题

试卷更新日期：2022-10-18 类型：月考试卷

进入出卷网下载

一、单选题

1. 关于x的方程 $(a - 1) x^{2} + 4 x - 3 = 0$ 是一元二次方程，则（）

A、 $a > 1$ B、 $a = 1$ C、 $a \neq 1$ D、 $a \geq 0$

查看试题解析
2. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，E为 $A D$ 边的中点， $A B =6$ ，则 $O E$ 的长为（）．

A、2 B、3 C、6 D、12

查看试题解析
3. 用配方法解方程 $x^{2} + 2 x - 2 = 0$ 时，配方结果正确的是（）．

A、 ${(x + 1)}^{2} = 3$ B、 ${(x + 1)}^{2} = 1$ C、 ${(x + 2)}^{2} = 3$ D、 ${(x + 2)}^{2} = 1$

查看试题解析
4. 下列说法正确的是（　　　）

A、对角线互相垂直的四边形是菱形 B、邻边相等的矩形是正方形 C、对角线相等的平行四边形是正方形 D、有一个内角是直角的四边形是矩形

查看试题解析
5. 已知m是一元二次方程 $x^{2} + 4 x - 1011 = 0$ 的一个根，则 $2 m^{2} + 8 m + 1$ 的值是（）．

A、-2022 B、-2023 C、2022 D、2023

查看试题解析
6. 如图，在矩形 $A B C D$ 中， $A B = 2 cm$ ，对角线 $A C$ 与 $B D$ 相交于点O， $D E ⊥ A C$ ，垂足为E， $O E = C E$ ，则 $B C$ 的长为（）．

A、 $2 \sqrt{3} cm$ B、 $4 cm$ C、 $2 \sqrt{5} cm$ D、 $2 \sqrt{2} cm$

查看试题解析
7. 如图，在正方形 $A B C D$ 中，E为 $A D$ 上一点，连接 $B E$ ， $B E$ 交对角线 $A C$ 于点F，连接 $D F$ ，若 $∠ A B E = 30 °$ ，则 $∠ C F D$ 的度数为（）．

A、 $45 °$ B、 $70 °$ C、 $75 °$ D、 $80 °$

查看试题解析
8. 已知关于x的一元二次方程 $(p + 1) x^{2} + 2 q x + (p + 1) = 0$ （其中p，q为常数）有两个相等的实数根，则下列结论中，错误的是（）．

A、1可能是方程 $x^{2} + q x + p = 0$ 的根 B、 $- 1$ 可能是方程 $x^{2} + q x + p = 0$ 的根 C、0可能是方程 $x^{2} + q x + p = 0$ 的根 D、1和-1都是方程 $x^{2} + q x + p = 0$ 的根

查看试题解析

二、填空题

9. 方程 $2 x^{2} + 3 x - 4 = 0$ 的二次项系数为．

查看试题解析
10. 如图，在菱形 $A B C D$ 中， $∠ A = 40 °$ ，则 $∠ C B D$ 的度数为．

查看试题解析
11. 已知关于x的一元二次方程 $x^{2} + 4 x + m = 0$ 有两个相等的实数根，则m的值为．

查看试题解析

12. 观察表格，一元二次方程

x^{2} - x - 1.1 = 0

的一个解的取值范围是．

x	1.3	1.4	1.5	1.6	1.7	1.8	1.9
$x^{2} - x - 1.1$	-0.71	-0.54	-0.35	-0.14	0.09	0.34	0.61

查看试题解析

13. 边长为2的一个正方形和一个等边三角形按如图所示的方式摆放，则 $△ A B C$ 的面积为．

查看试题解析

三、解答题

14. 解方程： $x^{2} - 4 x + 3 = 0$ ．

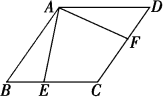
查看试题解析
15. 如图，点E，F分别在菱形ABCD的边BC，CD上，且∠BAE＝∠DAF．求证：AE＝AF．

查看试题解析
16. 用公式法解方程： $m^{2} - 3 m - 1 = 0$ ．

查看试题解析
17. 如图，在矩形 $A B C D$ 中，F是边 $B C$ 上的一点，请在边 $A D$ 上求作一点H，连接 $H F$ ，使得四边形 $B E H F$ 为平行四边形．（保留作图痕迹，不写作法）

查看试题解析
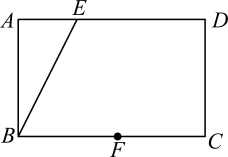18. 以下是某同学解方程 $x^{2} - 3 x = - 2 x + 6$ 的过程：
解：方程两边因式分解，得 $x (x - 3) = - 2 (x - 3)$ ， ①

方程两边同除以 $(x - 3)$ ，得 $x = - 2$ ， ②

∴原方程的解为 $x = - 2$ ． ③

(1)、上面的运算过程第步出现了错误．

(2)、请你写出正确的解答过程．

查看试题解析
19. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，过点B作 $B E ∥ A C$ ，且 $B E = \frac{1}{2} A C$ ，连接 $E C$ ，求证：四边形 $B E C O$ 是矩形．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - (2 k - 1) x + k^{2} - k - 2 = 0$ ．

(1)、求证：无论k为何值，方程都有两个不相等的实数根．

(2)、若方程有一个根为 $- 2$ ，求k的值．

查看试题解析
21. 如图，一矩形草坪的长为25米，宽为12米，在草坪上有两条互相垂直且宽度相等的矩形小路（阴影部分），非阴影部分的面积是230平方米．

(1)、求小路的宽．

(2)、每平方米小路的建设费用为200元，求修建两条小路的总费用．

查看试题解析
22. 如图，四边形 $A B C D$ 是平行四边形，对角线 $A C$ ， $B D$ 交于点O， $A C = 2 A B$ ， $B E ∥ A C ， O E ∥ A B$ ．

(1)、求证：四边形 $A B E O$ 是菱形．

(2)、若 $A C = 4 \sqrt{5}$ ， $B D = 8$ ，求四边形 $A B E O$ 的面积．

查看试题解析
23. 阅读下面的材料，解答问题．
材料：解含绝对值的方程： $x^{2} - 3 | x | - 10 = 0$ ．

解：分两种情况：

①当 $x \geq 0$ 时，原方程化为 $x^{2} - 3 x - 10 = 0$ ，解得 $x_{1} = 5$ ， $x_{2} = - 2$ （舍去）；

②当 $x < 0$ 时，原方程化为 $x^{2} + 3 x - 10 = 0$ ，解得 $x_{3} = - 5$ ， $x_{4} = 2$ （舍去）．

综上所述，原方程的解是 $x_{1} = 5$ ， $x_{2} = - 5$ ．

请参照上述方法解方程 $x^{2} - | x + 1 | - 1 = 0$ ．

查看试题解析

24. 关于x的一元二次方程

x^{2} + b x + c = 0

经过适当变形，可以写成

(x - s) (x - t) = p (s \leq t)

的形式．现列表探究

x^{2} - 4 x - 5 = 0

的变形：

变形	s	t	p
$(x + 1) (x - 5) = 0$	-1	5	0
$x (x - 4) = 5$	0	4	5
$(x - 1) (x - q) = 8$	1	q	8
${(x - 2)}^{2} = 9$	2	2	9

回答下列问题：

(1)、表格中q的值为．

(2)、观察上述探究过程，表格中s与t满足的等量关系为．

(3)、记

x^{2} + b x + c = 0

的两个变形为

(x - s_{1}) (x - t_{1}) = p_{1}

和

(x - s_{2}) (x - t_{2}) = p_{2} (p_{1} \neq p_{2})

，求

\frac{t_{1} - t_{2}}{s_{1} - s_{2}}

的值．

查看试题解析

25. 如图1，在正方形 $A B C D$ 中，O是对角线的交点，P是线段 $A O$ 上任一点（不与点A，O重合），过点P作 $P E ⊥ P B$ ， $P E$ 交边 $C D$ 于点E．

(1)、 $∠ P C E$ 的度数为．

(2)、求证： $P B = P E$ ．

(3)、如图2，若正方形 $A B C D$ 的边长为4，过点E作 $E F ⊥ A C$ 于点F，在点P运动的过程中， $P F$ 的长度是否发生变化？若不发生变化，直接写出这个不变的值；若发生变化，请说明理由．

查看试题解析
26. 课本再现：

(1)、下图所示的是北师大版九年级上册数学课本上的一道题：

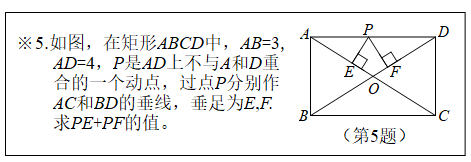
如图1，连接 $P O$ ，利用 $△ P A O$ 与 $△ P D O$ 的面积之和是矩形面积的 $\frac{1}{4}$ ，可求出 $P E + P F$ 的值，请你写出求解过程．

(2)、知识应用：
如图，在矩形 $A B C D$ 中，点M，N分别在边 $A D$ ， $B C$ 上，将矩形 $A B C D$ 沿直线 $M N$ 折叠，使点D恰好与点B重合，点C落在点 $C^{'}$ 处．

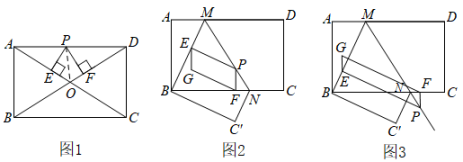
①如图2，P为线段 $M N$ 上一动点（不与点M，N重合），过点P分别作直线 $B M$ ， $B C$ 的垂线，垂足分别为E和F，以 $P E$ ， $P F$ 为邻边作平行四边形 $P E G F$ ，若 $D M = 13$ ， $C N = 5$ ，求 $▱ P E G F$ 的周长．

②如图3，当点P在线段 $M N$ 的延长线上运动时，若 $D M = m$ ， $C N = n$ ．请用含m，n的式子直接写出 $G F$ 与 $G E$ 之间的数量关系．

查看试题解析