浙江省温州市十二中2022-2023学年九年级上学期9月份检测数学试题
试卷更新日期:2022-10-18 类型:月考试卷
一、精心选一选(本题有10小题,每小题4分,共40分。)
-
1. 下列事件中是必然事件的是( )A、掷一枚硬币,正面朝上 B、某运动员跳高的最好成绩是20.1米 C、太阳从东方升起 D、从车间刚生产的产品中任意抽取一件是次品2. 下列函数关系中,y是x的二次函数的是( )A、y B、y=5x+3 C、y=x2﹣3 D、y3. 抛物线y=2(x﹣1)2+3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,﹣3) D、(﹣1,﹣3)4. 抛物线y=x2+4x+4与x轴的交点个数为( )A、0个 B、1个 C、2个 D、3个5. 如果将抛物线y=2(x﹣1)2向左平移2个单位,再向下平移2个单位后所得新抛物线的表达式是( )A、y=2(x﹣3)2﹣2 B、y=2(x﹣3)2+2 C、y=2(x+1)2﹣2 D、y=2(x+1)2+26. 已知(﹣2,y1),(1,y2),(3,y3)是抛物线y=(x)2+c上的点,则( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y2<y1 D、y1<y3<y27. 已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有9个,黑球有n个,若随机从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀,经过大量重复试验发现摸出黑球的频率稳定在0.4附近,则n的值为( )A、5 B、6 C、7 D、88. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象为( )A、
 B、
B、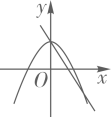 C、
C、 D、
D、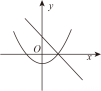 9. 关于二次函数y=x2﹣4x+3,下列说法错误的是( )A、当x<1时,y随x的增大而减小 B、它的图象与x轴有交点 C、当1<x<3时,y>0 D、它的图象与y轴交于点(0,3)10. 已知二次函数y=x2+bx,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣2<x<3的范围内有解,则t的取值范围是( )A、t≥﹣1 B、﹣1≤t<3 C、3<t<8 D、﹣1≤t<8
9. 关于二次函数y=x2﹣4x+3,下列说法错误的是( )A、当x<1时,y随x的增大而减小 B、它的图象与x轴有交点 C、当1<x<3时,y>0 D、它的图象与y轴交于点(0,3)10. 已知二次函数y=x2+bx,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣2<x<3的范围内有解,则t的取值范围是( )A、t≥﹣1 B、﹣1≤t<3 C、3<t<8 D、﹣1≤t<8二、认真填一填(本题有6小题,每小题5分,共30分)
-
11. 从﹣1,0,2和3中随机地选一个数,则选到正数的概率是 .12. 已知关于x的二次函数y=(m+2)x2+2x﹣3的图象开口向下,则m的取值范围是 .13. 已知二次函数y=2x2+bx+3的对称轴为直线x=﹣2,则b= .14. 如图所示,一个运动员推铅球,铅球在点A处出手,铅球落地点在B处,已知铅球经过的路线是抛物线y(x﹣4)2+3,则铅球的落地点B到运动员的水平距离为 米.
 15. 如图,抛物线y=x2﹣2x+m的顶点为A,与y轴交于点B,BC∥x轴,与抛物线交于点C,CD∥y轴,与射线OA交于点D,OC=OD,则m= .
15. 如图,抛物线y=x2﹣2x+m的顶点为A,与y轴交于点B,BC∥x轴,与抛物线交于点C,CD∥y轴,与射线OA交于点D,OC=OD,则m= . 16. “水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图1所示,碗体DEC呈抛物线状(碗体厚度不计),点E是抛物线的顶点,碗底高EF=1cm,碗底宽AB=2cm,当瓷碗中装满面汤时,液面宽CD=8cm,此时面汤最大深度EG=6cm,将瓷碗绕点B缓缓倾斜倒出部分面汤如图2,当∠ABK=30°时停止,此时液面CH宽为 cm;碗内面汤的最大深度是 cm.
16. “水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图1所示,碗体DEC呈抛物线状(碗体厚度不计),点E是抛物线的顶点,碗底高EF=1cm,碗底宽AB=2cm,当瓷碗中装满面汤时,液面宽CD=8cm,此时面汤最大深度EG=6cm,将瓷碗绕点B缓缓倾斜倒出部分面汤如图2,当∠ABK=30°时停止,此时液面CH宽为 cm;碗内面汤的最大深度是 cm.
三、解答题(本题有8小题,共80分,)
-
17. 已知抛物线y=x2+bx+c经过点(1,0),(0,﹣4).(1)、求这个抛物线的函数表达式;(2)、判断点(2,7)是否在抛物线上.18. 一个不透明的袋子中装有2个红球和1个白球,这些球除颜色外其余都相同,先从袋中摸出1个球后不放回,再摸出一个球.(1)、请用树状图或列表法列举出两次摸球可能出现的各种结果;(2)、求两次摸到不同颜色的球的概率.19. 已知二次函数y=x2﹣4x+3.
 (1)、把二次函数化成y=a(x﹣h)2+k的形式;(2)、在平面直角坐标系xOy中画出该函数的图象;(3)、当0≤x≤3时,y的取值范围是 .20. 对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频率表如下:
(1)、把二次函数化成y=a(x﹣h)2+k的形式;(2)、在平面直角坐标系xOy中画出该函数的图象;(3)、当0≤x≤3时,y的取值范围是 .20. 对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频率表如下:抽取件数
50
100
150
200
500
800
1000
合格频数
42
88
141
176
445
724
901
合格频率
0.84
a
0.94
0.88
0.89
0.91
b
(1)、计算表中a,b的值并估计任抽一件衬衣是合格品的概率.(2)、估计出售2000件衬衣,其中次品大约有几件.21. 某游乐场的圆形喷水池中心O有一喷水管OA,从点A四周喷水,喷出的水柱为抛物线,且形状相同,如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,水柱所在的抛物线(第一象限部分)的函数表达式为y(x﹣3)2+2. (1)、求喷水管高OA.(2)、身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?(3)、现重新改建喷泉,升高喷水管,使落水点与喷水管距离7m,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点3m处达到最高,则喷水管OA要升高多少?22. 某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏40米.
(1)、求喷水管高OA.(2)、身高为1.7m的小明站在距离喷水管4m的地方,他会被水喷到吗?(3)、现重新改建喷泉,升高喷水管,使落水点与喷水管距离7m,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点3m处达到最高,则喷水管OA要升高多少?22. 某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏40米. (1)、不考虑墙体长度,问长方形的各边的长为多少米时,长方形的面积最大?(2)、若11≤AB≤12,试求长方形面积S的取值范围.23. 2022年中秋节一过,某超市经盘点后发现其仓库剩余1150盒进价为80元的某品牌月饼,市场调查发现:若每盒以160元销售,接下来一周可销售300盒,售价每降低1元,可多销售10盒,设每盒降价x元(x为整数),记这种品牌月饼的周销售利润为W.(1)、请写出W与x之间的函数表达式.(2)、当售价降低多少元时,周销售利润最大?最大周销售利润为多少元?(3)、超市按利润最大销售一周后,发现仍有库存,计划在接下来一周内售完余下月饼,特向厂家争取了将余下月饼的进价每盒降低a元的优惠.若超市重新调整售价,希望在售完余下月饼时恰能获得最大利润,则a的最小值为 (直接写出结果).24. 如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连结PA,PF,AF.
(1)、不考虑墙体长度,问长方形的各边的长为多少米时,长方形的面积最大?(2)、若11≤AB≤12,试求长方形面积S的取值范围.23. 2022年中秋节一过,某超市经盘点后发现其仓库剩余1150盒进价为80元的某品牌月饼,市场调查发现:若每盒以160元销售,接下来一周可销售300盒,售价每降低1元,可多销售10盒,设每盒降价x元(x为整数),记这种品牌月饼的周销售利润为W.(1)、请写出W与x之间的函数表达式.(2)、当售价降低多少元时,周销售利润最大?最大周销售利润为多少元?(3)、超市按利润最大销售一周后,发现仍有库存,计划在接下来一周内售完余下月饼,特向厂家争取了将余下月饼的进价每盒降低a元的优惠.若超市重新调整售价,希望在售完余下月饼时恰能获得最大利润,则a的最小值为 (直接写出结果).24. 如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连结PA,PF,AF.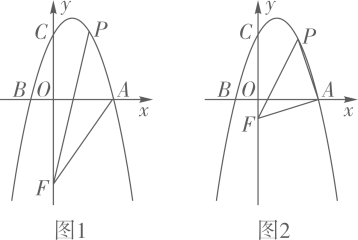 (1)、求该抛物线所对应的函数表达式;(2)、如图1,当点F的坐标为(0,﹣4),求出此时△AFP面积的最大值;(3)、如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
(1)、求该抛物线所对应的函数表达式;(2)、如图1,当点F的坐标为(0,﹣4),求出此时△AFP面积的最大值;(3)、如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.