浙江省杭州市拱墅区锦绣育才教育集团2022-2023学年八年级上学期数学9月月考试题
试卷更新日期:2022-10-18 类型:月考试卷
一、选择题(本大题有10个小题,每小题3分,共30分)
-
1. 下面四个图形分别是低碳、节水、节能和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式﹣x<2的最小整数解( )A、﹣3 B、﹣1 C、0 D、13. 下列长度的三条线段能构成三角形的是( )A、3,1,2 B、2,3,6 C、5,8,15 D、9,9,14. 一个三角形三个内角的度数之比为3:4:5,这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形5. 如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )A、
2. 不等式﹣x<2的最小整数解( )A、﹣3 B、﹣1 C、0 D、13. 下列长度的三条线段能构成三角形的是( )A、3,1,2 B、2,3,6 C、5,8,15 D、9,9,14. 一个三角形三个内角的度数之比为3:4:5,这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形5. 如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )A、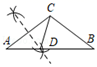 B、
B、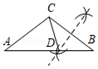 C、
C、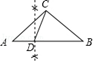 D、
D、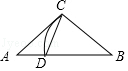 6. 若一个等腰三角形的一条边是另一条边的k倍,我们把这样的等腰三角形叫做“k倍边等腰三角形”.如果一个等腰三角形是“4倍边等腰三角形”,且周长为18cm,则该等腰三角形底边长为( )A、12cm B、12cm或2cm C、2cm D、4cm或12cm7. 如图,在△ABC中,AD平分∠BAC,AE⊥BC,已知∠BAC=2∠B,∠B=4∠DAE,那么∠C的度数为( )
6. 若一个等腰三角形的一条边是另一条边的k倍,我们把这样的等腰三角形叫做“k倍边等腰三角形”.如果一个等腰三角形是“4倍边等腰三角形”,且周长为18cm,则该等腰三角形底边长为( )A、12cm B、12cm或2cm C、2cm D、4cm或12cm7. 如图,在△ABC中,AD平分∠BAC,AE⊥BC,已知∠BAC=2∠B,∠B=4∠DAE,那么∠C的度数为( )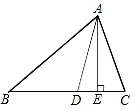 A、45° B、60° C、70° D、72°8. 若不等式组 的解集为x<﹣m,则下列各式正确的是( )A、m≥n B、m≤n C、m>n D、m<n9. 把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本.则共有学生( )A、4人 B、5人 C、6人 D、5人或6人10. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF,其中正确的是( )
A、45° B、60° C、70° D、72°8. 若不等式组 的解集为x<﹣m,则下列各式正确的是( )A、m≥n B、m≤n C、m>n D、m<n9. 把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本.则共有学生( )A、4人 B、5人 C、6人 D、5人或6人10. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF,其中正确的是( )
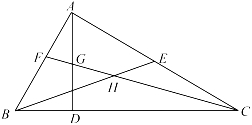 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题(本大题有6个小题,每小题4分,共24分)
-
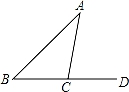
11. 若3a<2a,则a﹣1 0(填“>”或“<”).12. 如图,已知在△ABC中,∠A=35°,其外角∠ACD=80°,则∠B=度.
 13. 命题“等腰三角形的两个底角相等.”的逆命题是 .14. 若关于x的不等式组 有且仅有2个整数解,则a的取值范围是 .15. 在△ABC中,AB=6,AC=8,S△ABC=26,∠ABC和∠ACB的角平分线交于点D,作DE⊥BC于E,若DE=2,则BC的长为 .16. 如图,已知∠AOB=α( 0°<α<60° ),射线OA上一点M,以OM为边在OA下方作等边△OMN,点P为射线OB上一点,若∠MNP=α,则∠OMP=.
13. 命题“等腰三角形的两个底角相等.”的逆命题是 .14. 若关于x的不等式组 有且仅有2个整数解,则a的取值范围是 .15. 在△ABC中,AB=6,AC=8,S△ABC=26,∠ABC和∠ACB的角平分线交于点D,作DE⊥BC于E,若DE=2,则BC的长为 .16. 如图,已知∠AOB=α( 0°<α<60° ),射线OA上一点M,以OM为边在OA下方作等边△OMN,点P为射线OB上一点,若∠MNP=α,则∠OMP=.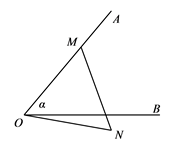
三、解答题(本大题有7个小题,共66分)
-
17. 解下列不等式(组).(1)、3(x﹣1)﹣5<2x;(2)、18.(1)、若x>y,比较﹣3x+5与﹣3y+5的大小,并说明理由;(2)、若x>y,且(a﹣3)x<(a﹣3)y,求a的取值范围.19. 如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AE=CF.
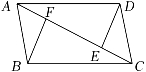 (1)、求证:△ABF≌△CDE;(2)、若∠BCF=30°,∠CBF=72°,求∠CED的度数.20. 已知关于x、y的二元一次方程组 (k为常数).(1)、求这个二元一次方程组的解(用含k的代数式表示);(2)、若方程组的解x、y满足x+y>5,求k的取值范围;(3)、若k≤1,设m=2x﹣3y,且m为正整数,求m的值.21. 在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.
(1)、求证:△ABF≌△CDE;(2)、若∠BCF=30°,∠CBF=72°,求∠CED的度数.20. 已知关于x、y的二元一次方程组 (k为常数).(1)、求这个二元一次方程组的解(用含k的代数式表示);(2)、若方程组的解x、y满足x+y>5,求k的取值范围;(3)、若k≤1,设m=2x﹣3y,且m为正整数,求m的值.21. 在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.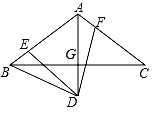 (1)、求证:△ABD是等边三角形;(2)、求证:BE=AF.22. 为了抓住世博会商机,某商店决定购进A、B两种世博会纪念品,若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.(1)、求购进A、B两种纪念品每件各需多少元?(2)、若该商店决定拿出4000元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B钟纪念品数量的8倍,那么该商店共有几种进货方案?(3)、若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少?23. 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连结AD,作∠ADE=40°,DE交线段AC于点E.
(1)、求证:△ABD是等边三角形;(2)、求证:BE=AF.22. 为了抓住世博会商机,某商店决定购进A、B两种世博会纪念品,若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.(1)、求购进A、B两种纪念品每件各需多少元?(2)、若该商店决定拿出4000元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B钟纪念品数量的8倍,那么该商店共有几种进货方案?(3)、若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少?23. 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连结AD,作∠ADE=40°,DE交线段AC于点E.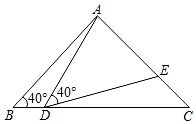 (1)、当∠BDA=115°时,∠BAD=°,∠DEC=°;(2)、当DC=AB=2时,△ABD与△DCE是否全等?请说明理由;(3)、在点D运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠AED的度数;若不可以,请说明理由.
(1)、当∠BDA=115°时,∠BAD=°,∠DEC=°;(2)、当DC=AB=2时,△ABD与△DCE是否全等?请说明理由;(3)、在点D运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠AED的度数;若不可以,请说明理由.