陕西省西安市新城区2022-2023学年八年级上学期第一次月考数学试题

试卷更新日期：2022-10-18 类型：月考试卷

进入出卷网下载

一、单选题

1. 在实数 $- \sqrt{\frac{1}{4}}$ ， 0， $π$ ， $\frac{\sqrt{2}}{2}$ ， 0.1020020002， $\frac{11}{7}$ ， 4.1515515551…（相邻两个1之间依次多一个5）中，无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 已知的三个内角分别为∠A、∠B、∠C，三边分别为a、b、c，下列条件不能判定△ABC为直角三角形的是（）

A、∠A：∠B：∠C=3：4：5 B、∠A=∠B-∠C C、 $b^{2} = (a + c) (a - c$ ) D、a：b：c=7：24：25

查看试题解析
3. 2021年9月15日，中华人民共和国第十四届运动会开幕式在西安奥体中心举行，如图，如果将西安钟楼的位置记为直角坐标系的原点，下列哪个点的位置可以表示奥体中心的位置（）

A、(－2，3) B、(2，3) C、(－2，－3) D、(2，－3)

查看试题解析
4. 估计 $\sqrt{3} \times \sqrt{6}$ 的值应在（）

A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间

查看试题解析
5. 平面直角坐标系中，已知点A（-3，2），B（x，y），且AB//x轴，若点B到y轴的距离是到x轴距离的2倍，则点B的坐标为（）.

A、（4，2）或（-4， 2） B、（-4，2）或（-4，-2） C、（4，2）或（4，-2） D、（-4，-2）或（4，-2）

查看试题解析
6. 下列各式计算正确的是（）

A、 $\sqrt{3} - \sqrt{2} = \sqrt{6}$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $\sqrt{2} \cdot \sqrt{2} = 2$

查看试题解析
7. 平面直角坐标系中，点A（﹣1，3），B（2，1），经过点A的直线a $∥$ x轴，点C是直线a上的一个动点，当线段BC的长度最短时，点C的坐标为（）

A、（﹣1，1） B、（3，2） C、（2，3） D、（2，﹣1）

查看试题解析
8. 已知Rt△BCE和Rt△ADE按如图方式摆放，∠A＝∠B＝90°，A、E、B在一条直线上，AD＝3，AE＝4，EB＝5，BC＝12，M是线段AD上的动点，N是线段BC上的动点，MN的长度不可能是（）

A、9 B、12 C、14 D、16

查看试题解析

二、填空题

9. $\sqrt{3}$ 的倒数为， 0.81的算术平方根是， $\sqrt{81}$ 的平方根是．

查看试题解析
10. 如图，Rt△MBC中，∠MCB＝90°，点M在数轴﹣1处，点C在数轴1处，MA＝MB，BC＝1，则数轴上点A对应的数是．

查看试题解析
11. 已知点P（2m-10，3m-9）在第二象限，且离x轴的距离为3，则点P坐标为．

查看试题解析
12. 已知y $= \sqrt{x - 2} + \sqrt{2 - x} + 3$ ，则 $y^{x}$ 的算术平方根是．

查看试题解析
13. 如图，在平面直角坐标系中，△OAB为等边三角形，AB丄x轴，AB=2，点C的坐标为（1，0），点P为OB边上的一个动点，则PA+PC的最小值为．

查看试题解析

三、解答题

14. 计算：

(1)、 $\sqrt{12} \times \sqrt{3} - 5$ ；

(2)、 $\sqrt{12} + \sqrt{\frac{1}{27}} + \sqrt{\frac{1}{3}}$ ；

(3)、 $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$ ；

(4)、 ${(3 - 2 \sqrt{5})}^{2} - (2 + 2 \sqrt{5}) \times (2 - 2 \sqrt{5})$ ．

查看试题解析
15. 求下列式子中的x：

(1)、25(x﹣ $\frac{3}{5}$ )²＝49；

(2)、 $\frac{1}{2}$ (x+1)²＝32．

查看试题解析
16. 如果一个正数x的两个平方根分别为a＋1和a－5.

(1)、求a和x的值；

(2)、求7x＋1的立方根.

查看试题解析
17. 已知点P $(\frac{3}{2} a + 2 ， 2 a - 3)$ ，根据下列条件，求出点P的坐标．

(1)、点P在y轴上；

(2)、点Q的坐标为（-3，3），直线PQ $∥$ x轴．

查看试题解析
18. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）.

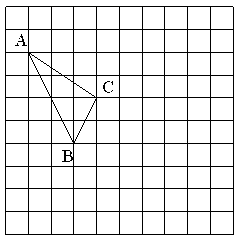
⑴请在如图所示的网格平面内作出平面直角坐标系；
⑵请作出△ABC关于y轴对称的△A′B′C′；
⑶写出点B′的坐标.

查看试题解析
19. 如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．

(1)、试说明：AF＝FC；

(2)、如果AB＝3，BC＝4，求AF的长．

查看试题解析
20. 像 $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) = 3$ 、 $\sqrt{a} \cdot \sqrt{a} = a (a \geq 0)$ 、 $(\sqrt{b} + 1) (\sqrt{b} - 1) = b - 1 (b \geq 0) \dots \dots$ 两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式．

(1)、请写出以下代数式的一个有理化因式： $\sqrt{a} + \sqrt{b} (a \geq 0 ， b \geq 0)$ ， $2 \sqrt{3} - 3 \sqrt{5}$ ；

(2)、化简： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2021} + \sqrt{2020}}$ ；

(3)、当 $2 \leq a \leq 4$ 时，直接写出代数式 $\sqrt{a + 2} - \sqrt{a + 1}$ 的最大值：．

查看试题解析
21. 如图所示，在平面直角坐标系中，在 $△$ ABC中，OA＝2，OB＝4，点C的坐标为(0，3).

(1)、求A，B两点坐标及 $S_{△ A B C}$ ；

(2)、若点M在x轴上，且 $S_{△ A C M} = \frac{2}{3} S_{△ A B C}$ ，试求点M的坐标.

(3)、若点D是第一象限的点，且满足 $△$ CBD是以BC为直角边的等腰直角三角形，请直接写出满足条件的点D的坐标.

查看试题解析
22. 如图，圆柱形容器的高为0.7m，底而周长为4.8m，在容器内壁离容器底部0.1m的点B处有一只蚊子，此时一只壁虎正好在容器外壁离容器上沿0.1m与蚊子相对的点A处，则壁虎捕捉蚊子的最短路程是多少？

查看试题解析
23. 阅读理解：亲爱的同学们，在以后的学习中我们会学习一个定理：直角三角形斜边上的中线等于斜边的一半．即：如图1：在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ，若点 $D$ 是斜边 $A B$ 的中点，则 $C D = \frac{1}{2} A B$ ．

(1)、牛刀小试：在图1中，若 $A C = 6$ ， $B C = 8$ ，其他条件不变，则 $C D =$ ；

(2)、活学活用：如图2，已知 $∠ A B C = ∠ A D C = 90 °$ ，点 $E$ 、 $F$ 分别为 $A C$ 、 $B D$ 的中点， $A C = 26$ ， $B D = 24$ ．求 $E F$ 的长；

(3)、问题解决：为了提高全民健身环境，公园管理部门想要建一个形状如图3中的四边形 $A B C D$ ，其中， $∠ A B C = 90 °$ ， $∠ A D C = 60 °$ ， $A D = C D = 6$ 千米，要在公园的 $B$ 、 $D$ 之间铺设一条笔直的塑胶跑道，若跑道铺设成本每米200元，当 $B D$ 最大时，请问管理部门预算160万元够用吗？

查看试题解析