浙江省丽水市青田县七校联盟2021-2022学年八年级上学期期中数学试题
试卷更新日期：2022-10-18 类型：期中考试
一、单选题
-
1. 下面是科学防控新冠知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（ ）A、
B、
C、
D、
2. 有两根6cm ， 8cm的木棒，以这两根木棒做一个三角形，可以选用第三根木棒的长为（ ）A、2cm B、6cm C、14cm D、16cm3. 下列选项中，可以用来证明命题“若a2＞4，则a＞2”是假命题的反例是（ ）A、a＝﹣3 B、a＝﹣2 C、a＝2 D、a＝34. 如图，∠B=60°，∠ACD=100°，那么∠A=（ ）
A、30° B、40° C、50° D、60°5. 如图， ，下列条件中不能使 的是（ ）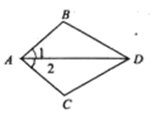
A、 B、 C、 D、6. 实数a，b，c在数轴上对应的点如图所示，则下列式子中正确的是（ ）
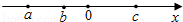A、a﹣c＞b﹣c B、a+c＜b+c C、ac＞bc D、7. 海曙区禁毒知识竞赛共有20道题，每一题答对得5分，答错或不答都扣2分，小明得分要超过80分，他至少要答对多少道题？如果设小明答对x道题，则他答错或不答的题数为20﹣x，根据题意得（ ）A、5x﹣2（20﹣x）≥80 B、5x﹣2（20﹣x）≤80 C、5x﹣2（20﹣x）>80 D、5x﹣2（20﹣x）<808. 如图，有一张直角三角形的纸片，两直角边AC＝6cm，BC＝8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上且与AE重合，则BD的长为（ ）
A、5cm B、4cm C、3cm D、2cm9. 如图，在△ABC中，∠ACB＝90°，分别以点A，B为圆心，大于AB长为半径作弧，两弧交于点M，N，作直线MN分别交AB，AC于点D，E，连接CD，BE．下列结论错误的是（ ）
A、AD＝CD B、BE＞CD C、∠BEC＝∠BDC D、BE平分∠CBD10. 如图，在一块含45°的三角板（∠ABC＝90°）右侧作以AC为斜边的Rt△ACD，过点B作AC的垂线，分别交AC、AD于点E、F，连接DE．设∠BFD＝α，∠BED＝β，则（ ）
A、3α＋2β＝600° B、3α－2β＝90° C、2α－β＝90° D、2α＋β＝360°二、填空题
-
11. x的3倍与7的和是正数，用不等式表示为 ．12. 命题“对顶角相等”的逆命题是13. 已知等腰三角形的周长20cm，一边长为8cm，则它的腰长是 ．14. 已知三角形 中 ，则斜边 上的高为.15. 不等式组 的最小整数解是.16. 如图，△ABC中，∠BAC＝100°，EF，MN分别为AB，AC的垂直平分线，则∠FAN＝ ．
17. 如图，点P是∠AOC的平分线上一点，PD⊥OA于D，且PD＝3，点M是射线OC上一动点，则PM的最小值为 ．
18. 在Rt△ABC中，∠C=90°，BC=8cm，AC=6cm，在射线BC上一动点D，从点B出发，以2厘米每秒的速度匀速运动，若点D运动t秒时，以A、D、B为顶点的三角形恰为等腰三角形，则所用时间t为秒．三、解答题
-
19. 已知：如图，在△ABC中，∠BAC＝80°，AD⊥BC于D，AE平分∠DAC，∠B＝60°，求∠C、∠DAE的度数．
20. 解下列不等式和不等式组，并把解集表示在数轴上．(1)、2（x＋1）≥3x－4(2)、21. 如图，AC和BD相交于点O，OA＝OC，OB＝OD．求证：
(1)、△AOB≌△COD．(2)、 ．22. 如图，BE、CF是锐角△ABC的两条高，M、N分别是BC、EF的中点，若EF=6，BC=10.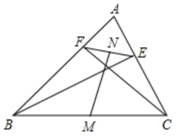
(1)、判断EF与MN的位置关系，并证明你的结论；(2)、求MN的长.23. 在创建文明城市的活动中，为更好的增强人们对垃圾分类的意识，某小区决定在其辖区内安装垃圾分类提示牌和垃圾箱，若购买3个垃圾分类提示牌和4个垃圾箱共需580元；购买5个垃圾分类提示牌和3个垃圾箱费用相同，(1)、求购买1个垃圾分类提示牌和1个垃圾箱各需多少元？(2)、若该小区需购买垃圾分类提示牌和垃圾箱共10个，计划投入费用不超过800元，问最多购买垃圾箱多少个？24. 【概念认识】如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．
(1)、【问题解决】
如图②，在△ABC中，∠A＝80°，∠B＝45°，若∠B的三分线BD交AC于点D，求∠BDC的度数；(2)、如图③，在△ABC中，BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，且∠BPC＝140°，求∠A的度数；(3)、【延伸推广】
在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A＝m°（），∠B＝54°，直接写出∠BPC的度数．（用含m的代数式表示）