浙教版数学九年级下册1.1锐角三角函数同步训练

试卷更新日期：2022-10-17 类型：同步测试

进入出卷网下载

一、单选题

1. 实数 $t a n 45 °$ ， $\sqrt[3]{64}$ ， $0$ ， $- π$ ， $\sqrt{9}$ ， $\frac{22}{7}$ ， $0.3131131113 \dots$ （相邻两个3之间依次多一个 1），其中无理数的个数是（）

A、4 B、2 C、1 D、3

查看试题解析
2. 计算sin 45°+cos45°的值为（）

A、1 B、2 C、 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
3. 如图，A、B、C是小正方形的顶点，且每个小正方形的边长为1，则tan∠BAC的值为（　　）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

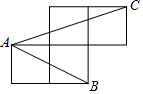查看试题解析
4. 如图，在菱形ABCD中，DE⊥AB，cosA＝ $\frac{3}{5}$ ， AE＝3，则tan∠DBE的值是（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
5. 已知正三角形外接圆半径为 $\sqrt{3}$ ，这个正三角形的边长是（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
6. 如图，直线y= $\frac{3}{4}$ x+3与x轴，y轴分别相交于A、B两点，则cos∠BAO的值是（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{5}{4}$

查看试题解析
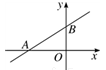7. 如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，且∠BCD＝30°，CD＝4 $\sqrt{3}$ ．则图中阴影部分的面积S_阴影＝（）

A、2π B、 $\frac{8}{3}$ π C、 $\frac{4}{3}$ π D、 $\frac{3}{8}$ π

查看试题解析
8. 如图，点A，B，C在正方形网格的格点上，则sin∠ABC＝（　　）

A、 $\frac{\sqrt{2}}{6}$ B、 $\frac{\sqrt{26}}{26}$ C、 $\frac{\sqrt{26}}{13}$ D、 $\frac{\sqrt{13}}{13}$

查看试题解析
9. 如图，在△ABC中，∠BAC＝90°，AB＝AC＝3 $\sqrt{6}$ cm，点D为△ABC内一点，∠CAD＝15°，AD＝4cm，连接CD，将△ACD绕点A顺时针旋转，使AC与AB重合，点D的对应点为点E，连接DE交AB于点F，则BF的长为（）

A、 $\frac{2 \sqrt{6}}{3}$ B、 $\frac{3 \sqrt{6}}{3}$ C、 $\frac{4 \sqrt{6}}{3}$ D、 $\frac{5 \sqrt{6}}{3}$

查看试题解析
10. 如图，在矩形ABCD中，AB＝8，BC＝12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，则sin∠ECF＝（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析

二、填空题

11. 如图，正方形网格中，点A，O，B，E均在格点上．⊙O过点A，E且与AB交于点C，点D是⊙O上一点，则 $t a n ∠ C D E =$ ．

查看试题解析
12. 如图，在Rt△ABC中，∠ACB= 90°，CD⊥AB于点D， AD= $\frac{9}{5}$ ， BD= $\frac{16}{5}$ ，则sinB=.

查看试题解析
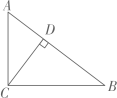13. △ABC内接于圆 $O$ ，且 $AB = AC$ ，圆 $O$ 的直径为 $10 cm$ ， $BC = 6 cm$ ，则 $sinB =$ .

查看试题解析
14. 规定： $s i n (- α) = - s i n α ， c o s (- α) = c o s α$ ， $s i n (α + β) = s i n α c o s β + c o s α s i n β$ ，据此判断下列等式成立的是：.（写出所有正确的序号）
①cos（﹣60°）＝ $- \frac{1}{2}$ ， ②sin75°＝ $\frac{\sqrt{6} + \sqrt{2}}{4}$ ， ③ $s i n 2 α = 2 s i n α c o s α$ ， ④ $s i n (α - β) = s i n α c o s β - c o s α s i n β$

查看试题解析
15. 如图，正方形ABCD中，点E，F分别为CD，DA延长线上的点，连接EF，BF，BE，BE交AD于点P，过点F作FK⊥BE垂足为G，FK与AB，CD分别交于点H，K，若DC=DE，∠EFB=∠FBC.则下列结论中：①BP＝HK；②∠ABF+∠FEB＝45°；③PG：GB：PE＝1：2：3；④ $\sin ∠ A B F = \frac{\sqrt{10}}{10}$ ；⑤若连接AG，则 $A H + A P = \sqrt{2} A G$ ；⑥HF²+HK²＝2HB².结论正确的有（只填序号）.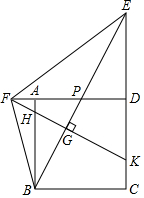

查看试题解析

三、综合题

16. 已知：在Rt△ABC 中，∠C=90°，sinA= $\frac{2}{3}$ ， AC=10，求△ABC的面积。

查看试题解析
17. 如图，在矩形ABCD中，E是BC边上的点，AE＝BC，DF⊥AE，垂足为F，连接DE．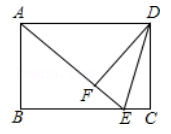

(1)、求证：△ABE≌△DFA；

(2)、如果AD＝10，AB＝6，求sin∠EDF的值．

查看试题解析
18. 如图，已知反比例函数 $y = \frac{k_{1}}{x}$ $(k_{1} > 0)$ 与一次函数 $y = k_{2} x + 1$ $(k_{2} \neq 0)$ 相交于 $A$ 、 $B$ 两点， $A C ⊥ x$ 轴于点 $C$ .若 $Δ O A C$ 的面积为 $1$ ，且 $t a n ∠ A O C = 2$ .

(1)、求出反比例函数与一次函数的解析式；

(2)、请直接写出 $B$ 点的坐标，并指出当 $x$ 在什么范围取值时，使 $\frac{k_{1}}{x} - (k_{2} x + 1) > 0$

查看试题解析
19. 在平面直角坐标系中，抛物线 $y = - x^{2} + k x - 2 k$ 的顶点为N.

(1)、若此抛物线过点A（ $- 3$ ， 1），求抛物线的解析式；

(2)、在（1）的条件下，若抛物线与y轴交于点B，连接AB，C为抛物线上一点，且满足CA=CB，求点C的坐标；

(3)、已知点M（ $2 - \frac{4 \sqrt{3}}{3}$ ， 0），且无论k取何值，抛物线都经过定点H，当∠MHN=60°时，求抛物线的解析式.

查看试题解析
20. 如图1，在矩形ABCD中，AB＝8，AD＝6，动点P沿着边AB从点A运动到点B，同时动点Q沿着边BC，CD从点B运动到点D，它们同时到达终点，BD与PQ交于点E．若记点Q的运动路程为x，线段BP的长记为y．

(1)、求y关于x的函数表达式．

(2)、如图2，当点Q在CD上时，求 $\frac{B E}{D E}$ ．

(3)、将矩形沿着PQ折叠，点B的对应点为点F，连结EF，当EF所在直线与△BCD的一边垂直时，求BP的长．

查看试题解析

浙教版数学九年级下册1.1锐角三角函数 同步训练

一、单选题

二、填空题

三、综合题

浙教版数学九年级下册1.1锐角三角函数同步训练