云南省临沧市凤庆县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-17 类型：期末考试

进入出卷网下载

一、填空题

1. 分解因式： $x y - x y^{3} =$ ．

查看试题解析
2. 要使式子 $\frac{3}{2 x + 1}$ 有意义，则x的取值范围是．

查看试题解析
3. 已知： ${(a - 2)}^{2} + | 2 b - 1 | = 0$ ，则 $a^{2017} \cdot b^{2018}$ 的值为．

查看试题解析
4. 一个多边形的内角和比它的外角和的3倍少180°，则这个多边形的边数是.

查看试题解析
5. 在△ABC中，CM是AB边上的中线，已知BC﹣AC=8cm，且△MBC的周长为30cm，则△AMC的周长为cm．

查看试题解析
6. 在等边ΔABC中，AB=4，BD平分∠ABC交AC于点D，点E在射线BC上，连接DE，∠DEC=30°，则CE的长为．

查看试题解析

二、单选题

7. 下列四个图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 下列运算正确的是（）

A、（-2）³=8 B、a²+b²=（a+b）² C、3a²·2a³=6a⁵ D、4x²-2x=2x

查看试题解析
9. 世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000000076克，将数0.000000076用科学记数法表示为（）

A、7.6×10^﹣⁹ B、7.6×10^﹣⁸ C、7.6×10⁹ D、7.6×10⁸

查看试题解析
10. 如图，在Rt△ABC中，斜边AB的垂直平分线交边AB于点E，交边BC于点D，如果∠ABC=26°，那么∠CAD的度数为（）

A、26° B、38° C、64° D、32°

查看试题解析
11. 如图，若BC=EC，∠BCE=∠ACD，则添加不能使△ABC≌△DEC的条件是（）

A、 $A B = D E$ B、 $∠ B = ∠ E$ C、 $A C = D C$ D、 $∠ A = ∠ D$

查看试题解析
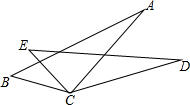12. 如图，D、E、F分别为BC、AD、BE的中点，若△BFD的面积为6，则△ABC的面积等于（）

A、36 B、18 C、48 D、24

查看试题解析
13. 施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原来计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则根据题意所列方程正确的是（）

A、 $\frac{2000}{x + 50} - \frac{2000}{x} = 2$ B、 $\frac{2000}{x} - \frac{2000}{x + 50} = 2$ C、 $\frac{2000}{x} - \frac{2000}{x - 50} = 2$ D、 $\frac{2000}{x - 50} - \frac{2000}{x} = 2$

查看试题解析
14. 如图，∠AOB=30°，P是∠AOB的角平分线上的一点，PM⊥OB于点M，PN//OB交OA于点N，若PM=1，则PN的长为（）

A、1 B、1.5 C、3 D、2

查看试题解析

三、解答题

15. 计算：

(1)、 $\sqrt{12} + {(- \frac{1}{2})}^{- 2} - | \sqrt{3} - 2 | - {(2 - \sqrt{3})}^{0} - \sqrt[3]{- 27}$

(2)、 $3 {(m - n)}^{2} - (2 m + n) (- n + 2 m)$

查看试题解析
16. 先化简分式 $(1 - \frac{1}{x - 2}) \div \frac{x^{2} - 6 x + 9}{2 x - 4}$ ，再从2≤x≤4中选一个合适的整数代入求值．

查看试题解析
17. 解方程：

(1)、 $\frac{3}{x} = \frac{2}{x - 2}$

(2)、 $\frac{2 x}{2 x - 1} + \frac{5}{1 - 2 x} = 3$

查看试题解析
18. 如图，在△ABC中，AD是△ABC的高线，AE是△ABC的角平分线。已知∠B=40°，∠C=70°.求∠DAE的度数.

查看试题解析
19. 用一条长21厘米的细绳围成一个等腰三角形.

(1)、如果腰长是底边的3倍，那么各边的长是多少？

(2)、能围成有一边的长是5厘米的等腰三角形吗？为什么？

查看试题解析
20. 如图，△ABC的三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）

(1)、请画出△ABC关于x轴成轴对称的图形△A₁B₁C₁ ，并写出A₁ ， B₁ ， C₁的坐标．

(2)、在y轴上找一点P，使PA+PB的值最小，请画出点P的位置．

(3)、若网格上的最小正方形边长为1，求△ABC的面积．

查看试题解析
21. 如图，在四边形ABCD中， $A D // B C$ ，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．求证：

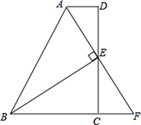(1)、FC＝AD；

(2)、AB＝BC+AD．

查看试题解析
22. 进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话∶
通过这段对话，请你求出该地驻军原来每天加固的米数．

查看试题解析
23. 如图1，点E、F分别是等边 $△ A B C$ 边 $A B$ 、 $B C$ 上的动点（端点除外），点E从顶点A向顶点B运动，点F从顶点B向顶点C运动，点E、F同时出发，且它们的运动速度相同，连接 $A F$ 、 $C E$ 交于点G．

(1)、求证： $△ A B F ≌ △ C A E$ ；

(2)、当点E、F分别在 $A B$ 、 $B C$ 边上运动时， $∠ F G C$ 变化吗？若变化请说明理由，若不变，求出它的度数；

(3)、如图2，若点E、F在运动到终点后继续在射线 $A B$ 、 $B C$ 上运动，直线 $A F$ 、 $E C$ 交点为G，则 $∠ F G C$ 变化吗？若变化请说明理由，若不变，求出它的度数．

查看试题解析