云南省红河州弥勒市2021-2022学年八年级上学期期末考试数学试题
试卷更新日期:2022-10-17 类型:期末考试
一、单选题
-
1. 如图,四个图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式由左边到右边的变形中,是分解因式的为( )A、 B、 C、 D、3. 下列各式运算正确的是( )A、 B、 C、 D、4. 如图,已知∠ABC=∠BAD , 再添加一个条件,仍不能判定△ABC≌△BAD的是( )
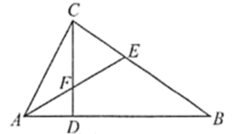
2. 下列各式由左边到右边的变形中,是分解因式的为( )A、 B、 C、 D、3. 下列各式运算正确的是( )A、 B、 C、 D、4. 如图,已知∠ABC=∠BAD , 再添加一个条件,仍不能判定△ABC≌△BAD的是( ) A、AC=BD B、∠C=∠D C、AD=BC D、∠ABD=∠BAC5. 如图1,从边长为 的正方形剪掉一个边长为 的正方形;如图2,然后将剩余部分拼成一个长方形.上述操作能验证的等式是( )
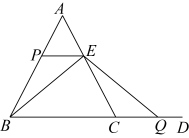
A、AC=BD B、∠C=∠D C、AD=BC D、∠ABD=∠BAC5. 如图1,从边长为 的正方形剪掉一个边长为 的正方形;如图2,然后将剩余部分拼成一个长方形.上述操作能验证的等式是( )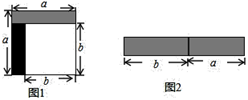 A、 . B、 . C、 . D、 .6. 现代科技的发展已经进入到了5G时代,温州地区将在2021年基本实现5G信号全覆盖.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输4千兆数据,5G网络比4G网络快360秒.若设4G网络的峰值速率为每秒传输x千兆数据,则由题意可列方程( )A、 — =360 B、 — =360 C、 — =360 D、 — =3607. 下列说法中,错误的是( )A、若分式的值为0,则x的值为3或-3 B、三角形具有稳定性,而四边形没有稳定性 C、锐角三角形的角平分线、中线、高均在三角形的内部 D、若一个正多边形的内角和为720°,则这个正多边形的每一个内角是120°8. 如图,的平分线与的垂直平分线相交于点 , , , 垂足分别为 , , , 则的值为( )
A、 . B、 . C、 . D、 .6. 现代科技的发展已经进入到了5G时代,温州地区将在2021年基本实现5G信号全覆盖.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输4千兆数据,5G网络比4G网络快360秒.若设4G网络的峰值速率为每秒传输x千兆数据,则由题意可列方程( )A、 — =360 B、 — =360 C、 — =360 D、 — =3607. 下列说法中,错误的是( )A、若分式的值为0,则x的值为3或-3 B、三角形具有稳定性,而四边形没有稳定性 C、锐角三角形的角平分线、中线、高均在三角形的内部 D、若一个正多边形的内角和为720°,则这个正多边形的每一个内角是120°8. 如图,的平分线与的垂直平分线相交于点 , , , 垂足分别为 , , , 则的值为( )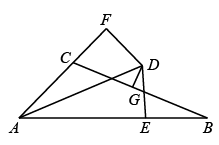 A、1 B、 C、2 D、3
A、1 B、 C、2 D、3二、填空题
-
9. 已知一粒米的质量约为0.000021kg,将这个数用科学记数法表示为 .10. 若 有意义,则x的取值范围是 .11. 已知是的三边长,满足 , 为偶数,则 .12. 如果将一副三角板按如图方式叠放,那么∠1的大小为 .
 13. 已知x+ =6,则x2+ =.14. 已知,等腰△ABC中,AB=AC,∠BAC=120°,P为直线BC上一点,BP=AB,则∠APB的度数为 .
13. 已知x+ =6,则x2+ =.14. 已知,等腰△ABC中,AB=AC,∠BAC=120°,P为直线BC上一点,BP=AB,则∠APB的度数为 .三、解答题
-
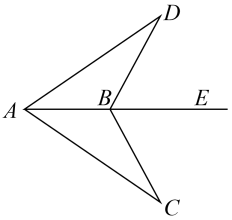
15. 计算:16. 先化简,再求值: , 其中 .17. 已知:如图,在和中, , 点在同一条直线上, .
求证: .
 18. 解方程: = ﹣2.19. 如图,在平面直角坐标系中:
18. 解方程: = ﹣2.19. 如图,在平面直角坐标系中: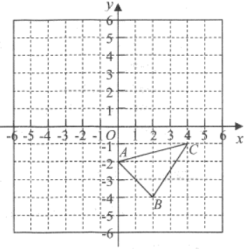
⑴请画出关于y轴对称的 , 并写、点的坐标;
⑵直接写出的面积为 ▲ ;
⑶在x轴上找一点P,使的值最小,请标出点P的在坐标轴上的位置.
20. 仔细阅读下面例题,解答问题:例题:已知二次三项式有一个因式是 , 求另一个因式以及的值.
解:设另一个因式为 , 得
则
∴
解得: ,
∴另一个因式为 , 的值为
问题:仿照以上方法解答下面问题:
已知二次三项式有一个因式是 , 求另一个因式以及的值.
21. 鲜花饼是以云南特有的食用玫瑰花入料的酥饼,是具有云南特色的云南经典点心代表.某超市购进两种口味的鲜花饼,其中种口味鲜花饼每盒的价格比种口味的鲜花饼贵10元,用800元购买种口味鲜花饼的数量与用600元购买种口味鲜花饼的数量相同.(1)、求购买的两种口味的鲜花饼每盒分别是多少元?(2)、若计划用不超过5000元的资金再次购进两种口味的鲜花饼共计150盒,已知两种口味的鲜花饼成本不变,求种口味的鲜花饼最多能购进多少盒?