云南省大理白族自治州祥云县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-17 类型：期末考试

进入出卷网下载

一、填空题

1. 已知点 $P$ （2，3）与点 $Q$ （m，n）关于 $y$ 轴对称，则m+n的值为．

查看试题解析
2. 因式分解： $a b^{2} - 2 a b + a =$ .

查看试题解析
3. 某种病菌的形状为球形，直径约是 $0.000000102 m$ ，用科学记数法表示这个数为．

查看试题解析
4. 如图， $A B // C D$ ，AE平分∠CAB交CD于点E，若 $∠ C = 70 °$ ，则 $∠ A E D =$ ．

查看试题解析
5. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为.

查看试题解析
6. 观察下列一组数： $\frac{1}{4}$ ， $\frac{3}{9}$ ， $\frac{5}{16}$ ， $\frac{7}{25}$ ， $\frac{9}{36}$ ，…，它们是按一定规律排列的，那么这一组数的第n个数是．

查看试题解析

二、单选题

7. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
8. 已知三角形两边的长分别是5和12，则此三角形第三边的长可能是（）

A、6 B、7 C、15 D、18

查看试题解析
9. 下列计算正确的是（）

A、 $- a^{4} 2 \div a^{2} b = - a^{2} b$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 $- 3 a^{2} + 2 a^{2} = - a^{2}$

查看试题解析
10. 分式 $\frac{a b}{a - b}$ 中，a，b都扩大2倍，那么分式的值（）

A、不变 B、扩大为原来的2倍 C、扩大为原来的4倍 D、缩小为原来的 $\frac{1}{2}$

查看试题解析
11. 一块三角形玻璃被打碎后，店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃，能够全等的依据是（）

A、 $A S A$ B、 $A A S$ C、 $S A S$ D、 $S S S$

查看试题解析
12. 已知：如图，在ΔABC中，AB=AC，AB的垂直平分线DE，分别交AB、AC于点D、E．若AD=3，BC=5，则ΔBEC的周长为（）

A、8 B、10 C、11 D、13

查看试题解析
13. 某优秀毕业生向我校赠送1080本课外书，现用A、B两种不同型号的纸箱包装运送，单独使用B型纸箱比单独使用A型纸箱可少用6个；已知每个B型纸箱比每个A型纸箱可多装15本．若设每个A型纸箱可以装书x本，则根据题意列得方程为（）

A、 $\frac{1080}{x} = \frac{1080}{x - 15} + 6$ B、 $\frac{1080}{x} = \frac{1080}{x - 15} - 6$ C、 $\frac{1080}{x + 15} = \frac{1080}{x} - 6$ D、 $\frac{1080}{x + 15} = \frac{1080}{x} + 6$

查看试题解析
14. 如图，七边形ABCDEFG中，AB、ED的延长线交于点O，若∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（）

A、30° B、35° C、40° D、45°

查看试题解析

三、解答题

15. 计算：

(1)、 ${(- 3 a)}^{2} \cdot a + 6 a^{4} \div (- 2 a)$

(2)、 $(x - 1) (x + 3) + {(x - 1)}^{2}$

查看试题解析
16. 解方程： $\frac{2 x}{x - 1} - 1 = \frac{4}{1 - x}$ .

查看试题解析
17. 先化简，再求值： $(1 - \frac{1}{m + 2}) \div \frac{m^{2} + 2 m + 1}{2 m + 2}$ ，其中 $m = \sqrt{2} - 2$

查看试题解析
18. 如图，平面直角坐标系中A（﹣4，6），B（﹣1，2），C（﹣3，1）．

(1)、作出△ABC关于y轴对称的图形△A₁B₁C₁ ，并写出△A₁B₁C₁各顶点的坐标；

(2)、求△ABC的面积．

查看试题解析
19. 已知：如图，点E、F在CD上，且∠A=∠B，AC $∥$ BD，CF=DE．求证：ΔAEC≌ΔBFD．

查看试题解析
20. 在“旅游示范公路”建设的的中，工程队计划在海边某路段修建一条长 $1200 m$ 的步行道，由于采用新的施工方式平均每天修建步行道的长度是计划的1.5倍，结果提前5天完成任务，求计划平均每天修建的长度．

查看试题解析
21. 如图，在ΔABC中，∠ABC与∠ACB的角平分线交于点O，过点O作DE $∥$ BC，分别交AB、AC于点D、E．若ΔADE的周长为7，ΔABC的周长为12，求BC的长度．

查看试题解析
22. 先阅读，再解答．
例： $x^{2} + y^{2} - 2 x + 4 y + 5 = 0$ ，求 $x + y$ 的值．
解：∵ $x^{2} + y^{2} - 2 x + 4 y + 5 = 0$
∴ $（ x^{2} - 2 x + 1) + (y^{2} + 4 y + 4) = 0$
即 $（ x - 1)^{2} + {(y + 2)}^{2} = 0$
$∵ （ x - 1)^{2} \geq 0 ， (y + 2 ）^{2} \geq 0$
$∴ （ x - 1 ）^{2} = 0 ，（ y + 2 ）^{2} = 0$
$∴ x = 1 ， y = - 2$
$∴ x + y = - 1$

(1)、已知 $x^{2} + 4 y^{2} - 6 x + 4 y + 10 = 0$ ，求 $x y$ 的值；

(2)、已知 $a 、 b 、 c$ 为ΔABC的三边，且满足 $a^{2} + 2 b^{2} + c^{2} - 2 b (a + c) = 0 ，$ 判断ΔABC的形状，并说明理由．

查看试题解析
23. 点C是直线l₁上一点，在同一平面内，把一个等腰直角三角板ABC任意摆放，其中直角顶点C与点C重合，过点A作直线l₂⊥l₁ ，垂足为点M，过点B作l₃⊥l₁ ，垂足为点N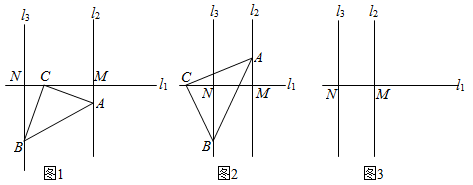

(1)、当直线l₂ ， l₃位于点C的异侧时，如图1，线段BN，AM与MN之间的数量关系(不必说明理由)；

(2)、当直线l₂ ， l₃位于点C的右侧时，如图2，判断线段BN，AM与MN之间的数量关系，并说明理由；

(3)、当直线l₂ ， l₃位于点C的左侧时，如图3，请你补全图形，并直接写出线段BN，AM与MN之间的数量关系.

查看试题解析