云南省大理白族自治州2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-17 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列每组数分别是三根木棒的长度,能用它们首尾相连摆成一个三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、5cm,5cm,11cm D、13cm,12cm,20cm3. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是0.00000000034m,这个数用科学记数法表示正确的是( )A、3.4×10-9 B、0.34×1010 C、3.4×10-10 D、3.4×10-114. 若一个正多边形的各个内角都是140°,则这个正多边形是( )A、正七边形 B、正八边形 C、正九边形 D、正十边形5. 为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中荧光棒共花费40元,缤纷棒共花费30元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为元( )A、 B、 C、 D、6. 如图,中, , , 是斜边上的高, , 则的长是( )
2. 下列每组数分别是三根木棒的长度,能用它们首尾相连摆成一个三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、5cm,5cm,11cm D、13cm,12cm,20cm3. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是0.00000000034m,这个数用科学记数法表示正确的是( )A、3.4×10-9 B、0.34×1010 C、3.4×10-10 D、3.4×10-114. 若一个正多边形的各个内角都是140°,则这个正多边形是( )A、正七边形 B、正八边形 C、正九边形 D、正十边形5. 为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中荧光棒共花费40元,缤纷棒共花费30元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为元( )A、 B、 C、 D、6. 如图,中, , , 是斜边上的高, , 则的长是( )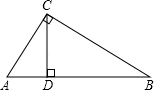 A、12 B、9 C、6 D、37. 如图,在 中, 是边 的垂直平分线,交 于点D,交 于点E,点P是直线 上的一个动点,若 ,则 的最小值为( )
A、12 B、9 C、6 D、37. 如图,在 中, 是边 的垂直平分线,交 于点D,交 于点E,点P是直线 上的一个动点,若 ,则 的最小值为( )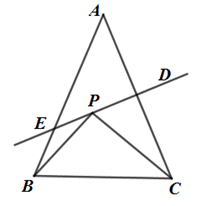 A、5 B、6 C、7 D、88. 观察下列树枝分叉的规律图,若第个图树枝数用表示,则( )
A、5 B、6 C、7 D、88. 观察下列树枝分叉的规律图,若第个图树枝数用表示,则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 分式有意义,则实数x的取值范围是 .10. 如图,△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是cm.
 11. 计算:=;12. 分解因式:x3y+2x2y+xy= .13. 如图,在中, , 以顶点为圆心,以适当长为半径画弧,分别交 , 于点、 , 再分别以点、为圆心,以大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是.
11. 计算:=;12. 分解因式:x3y+2x2y+xy= .13. 如图,在中, , 以顶点为圆心,以适当长为半径画弧,分别交 , 于点、 , 再分别以点、为圆心,以大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是.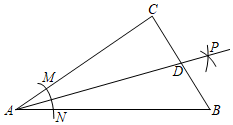 14. AE是△ABC的角平分线,AD是BC边上的高,且∠B=40°,∠ACD=70°,则∠DAE的度数为 .
14. AE是△ABC的角平分线,AD是BC边上的高,且∠B=40°,∠ACD=70°,则∠DAE的度数为 .三、解答题
-
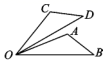
15. 解下列分式方程:(1)、(2)、16. 如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
 17. 先化简: ,再在﹣2,0,1,2四个数中选一个合适的数作为x的取值代入求值.18. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
17. 先化简: ,再在﹣2,0,1,2四个数中选一个合适的数作为x的取值代入求值.18. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1). (1)、在图中作出△ABC关于x轴的对称图形△A1B1C1 , 并写出点C1的坐标.(2)、求△ABC的面积.19. 如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形.
(1)、在图中作出△ABC关于x轴的对称图形△A1B1C1 , 并写出点C1的坐标.(2)、求△ABC的面积.19. 如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形. 20. 已知在△ABC中,D为边BC上一点,AB=AD=CD,BE平分∠ABC,交AC于点E.
20. 已知在△ABC中,D为边BC上一点,AB=AD=CD,BE平分∠ABC,交AC于点E. (1)、求证:∠ABC=2∠C;(2)、若AD平分∠BAC,求∠BAD的度数.21. 如图1是一个长为 , 宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形.
(1)、求证:∠ABC=2∠C;(2)、若AD平分∠BAC,求∠BAD的度数.21. 如图1是一个长为 , 宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形. (1)、图2中的阴影正方形边长表示正确的序号为;
(1)、图2中的阴影正方形边长表示正确的序号为;①;②;③.
(2)、由图2可以直接写出 , , 之间的一个等量关系是 ;(3)、根据(2)中的结论,解决下列问题: , , 求的值.22. 接种疫苗是阻断新冠病毒传播的有效途径,针对疫苗急需问题,某制药厂紧急批量生产,计划每天生产疫苗16万剂,但受某些因素影响,有10名工人不能按时到厂.为了应对疫情,回厂的工人加班生产,由原来每天工作8小时增加到10小时,每人每小时完成的工作量不变,这样每天只能生产疫苗15万剂.求该厂当前参加生产的工人有多少人?23. 如图 (1)、【问题解决】
(1)、【问题解决】已知△ABC中,AB=AC,D,A,E三点都在直线l上,且有∠BDA=∠AEC=∠BAC.如图①,当∠BAC=90°时,线段DE,BD,CE的数量关系为:;
(2)、【类比探究】如图②,在(1)的条件下,当0°<∠BAC<180°时,线段DE,BD,CE的数量关系是否变化,若不变,请证明:若变化,写出它们的关系式;
(3)、【拓展应用】如图③,AC=BC,∠ACB=90°,点C的坐标为(-2,0),点B的坐标为(1,2),请求出点A的坐标.