云南省保山市隆阳区2021-2022学年八年级上学期期末考试数学试题
试卷更新日期:2022-10-17 类型:期末考试
一、单选题
-
1. 观察下列平面图形,其中是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 将下列长度的三条线段首尾顺次相接,能组成三角形的是 ( )A、1cm,2 cm,3 cm B、2 cm,3 cm,5 cm C、5cm,6 cm,10 cm D、25cm,12 cm,11 cm3. 六边形的内角和是( )A、180° B、360° C、540° D、720°4. 如图,已知 ,添加下列条件不能判定 的是( )
A、1个 B、2个 C、3个 D、4个2. 将下列长度的三条线段首尾顺次相接,能组成三角形的是 ( )A、1cm,2 cm,3 cm B、2 cm,3 cm,5 cm C、5cm,6 cm,10 cm D、25cm,12 cm,11 cm3. 六边形的内角和是( )A、180° B、360° C、540° D、720°4. 如图,已知 ,添加下列条件不能判定 的是( ) A、 B、 C、 D、5. 若 , 两点关于轴对称,则的值是( )A、2 B、-2 C、6 D、-66. 下列运算正确的是( )A、 B、 C、 D、7. 下列从左到右的变形中,是分解因式的是( )A、 B、 C、 D、8. 随着市场对新冠疫苗需求越来越大,为满足市场需求,某大型疫苗生产企业更新技术后,加快了生产速度,现在平均每天比更新技术前多生产10万份疫苗,现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间相同,设更新技术前每天生产x万份,依据题意得( )A、 B、 C、 D、
A、 B、 C、 D、5. 若 , 两点关于轴对称,则的值是( )A、2 B、-2 C、6 D、-66. 下列运算正确的是( )A、 B、 C、 D、7. 下列从左到右的变形中,是分解因式的是( )A、 B、 C、 D、8. 随着市场对新冠疫苗需求越来越大,为满足市场需求,某大型疫苗生产企业更新技术后,加快了生产速度,现在平均每天比更新技术前多生产10万份疫苗,现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间相同,设更新技术前每天生产x万份,依据题意得( )A、 B、 C、 D、二、填空题
-
9. 如图,△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积.
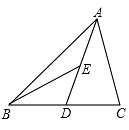 10. 如图所示,中, , AD平分 , 垂足为E, , , 则BE的长为 .
10. 如图所示,中, , AD平分 , 垂足为E, , , 则BE的长为 . 11. 纳米是一种长度单位,常用于度量物质原子的大小,1纳米=10-9米,已知某植物孢子的直径为45000纳米,用科学记数法表示该孢子的直径为米.12. 已知x+ =5,那么x2+ = .13. 对于两个非零代数式,定义一种新的运算: . 若 , 则 .14. 已知等腰三角形的两边长分别为4和6,则它的周长等于
11. 纳米是一种长度单位,常用于度量物质原子的大小,1纳米=10-9米,已知某植物孢子的直径为45000纳米,用科学记数法表示该孢子的直径为米.12. 已知x+ =5,那么x2+ = .13. 对于两个非零代数式,定义一种新的运算: . 若 , 则 .14. 已知等腰三角形的两边长分别为4和6,则它的周长等于三、解答题
-
15. 先化简,再求值:(3x-y)2+(3x+y)(3x-y) ,其中x=1,y=-2.16. 如图,已知A,B,C,D四点在同一直线上,AM∥CN,BM=DN,∠M=∠N,求证:AC=BD.
 17. 解下列分式方程:(1)、(2)、18. 如图所示,在平面直角坐标系.各顶点的坐标分别为: , ,
17. 解下列分式方程:(1)、(2)、18. 如图所示,在平面直角坐标系.各顶点的坐标分别为: , , (1)、在图中作 , 使和关于x轴对称;(2)、写出点的坐标;(3)、求的面积.19. 分解因式:(1)、(2)、20. 如图所示,E、F分别是的边AB、BC上一点,连接EF并延长交AC的延长线于点D. , , , 求的度数.
(1)、在图中作 , 使和关于x轴对称;(2)、写出点的坐标;(3)、求的面积.19. 分解因式:(1)、(2)、20. 如图所示,E、F分别是的边AB、BC上一点,连接EF并延长交AC的延长线于点D. , , , 求的度数. 21. 如图△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.求证:DB=DE.
21. 如图△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.求证:DB=DE.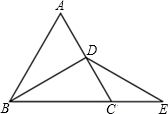 22. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?23. 如图1,点E、F分别是等边边、上的动点(端点除外),点E从顶点A向顶点B运动,点F从顶点B向顶点C运动,点E、F同时出发,且它们的运动速度相同,连接、交于点G.
22. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?23. 如图1,点E、F分别是等边边、上的动点(端点除外),点E从顶点A向顶点B运动,点F从顶点B向顶点C运动,点E、F同时出发,且它们的运动速度相同,连接、交于点G. (1)、求证:;(2)、当点E、F分别在、边上运动时,变化吗?若变化请说明理由,若不变,求出它的度数;(3)、如图2,若点E、F在运动到终点后继续在射线、上运动,直线、交点为G,则变化吗?若变化请说明理由,若不变,求出它的度数.
(1)、求证:;(2)、当点E、F分别在、边上运动时,变化吗?若变化请说明理由,若不变,求出它的度数;(3)、如图2,若点E、F在运动到终点后继续在射线、上运动,直线、交点为G,则变化吗?若变化请说明理由,若不变,求出它的度数.