安徽省合肥市蜀山区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-17 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点A (8，-2022）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 一次函数y=-x-2m (m为常数〉图象上有两点A( $\frac{3}{2}$ ， y₁)、B(2，y₂)，则y₁与y₂的大小关系是（）

A、y₁＞ y₂ B、y₁＜y₂ C、y₁=y₂ D、无法确定

查看试题解析
3. 下列垃圾分类的标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若三角形三个内角度数之比为3：4：9，则这个三角形一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形

查看试题解析
5. 已知等腰三角形的两边长分别为4和9，则此等腰三角形的周长为（）

A、17 B、22 C、17或22 D、12或27

查看试题解析
6. 如图，△ABC中，AB=6，AC=8，∠ABC与∠ACB的平分线BD、CD交于点D.过点D作EF∥BC，分别交AB，AC于点E，F，则△AEF的周长为（）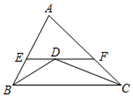

A、12 B、13 C、14 D、15

查看试题解析
7. 下列命题是假命题的是（）

A、对顶角相等 B、若|x|=1，则x=1 C、内错角相等，两直线平行 D、若x³=0，则x=0

查看试题解析
8. 如图，在四边形ABCD中，∠A=90°， AD=2，连接BD，BD⊥CD，∠ADB=∠C，若点P是BC边上一动点，则DP长的最小值为（）

A、2 B、4 C、6 D、8

查看试题解析
9. 元旦期间，李华到市体育馆进行体有锻炼，锻炼一段时间后返回家中，如图反映了这个过程中，李华离家的距离S（km）与时间t（h）之间的对应关系，根据图象，下列说法中：①体育馆与李华家之间的距离是6km；②李华在体育馆锻炼了2h；③李华从体育馆返回家中的平均速度是 $\frac{4}{3}$ km/h；④李华离家4k m时的时间是 $\frac{2}{3}$ h或 $\frac{7}{2}$ h．其中正确的说法是（）

A、①③ B、②④ C、①②③ D、①②④

查看试题解析
10. 如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，AD＜AB，且点E在线段CD上，则下列结论中不一定成立的是（）

A、△ABD≌△ACE B、BD⊥CD C、∠BAE-∠ABD=45° D、DE=CE

查看试题解析

二、填空题

11. 函数y= $\sqrt{4 - x}$ 中，自变量x的取值范围是

查看试题解析
12. 如图，在△ABC中，点D、E分别为边AC、BC上的点，且AD=DE，AB=BE，∠A=70°，则∠CED=度．

查看试题解析
13. 一次函数y=kx+b（k，b为常数且k≠0）的图象如图所示，且经过点(-2，0)，则关于x的不等式kx+b＞0的解集为

查看试题解析
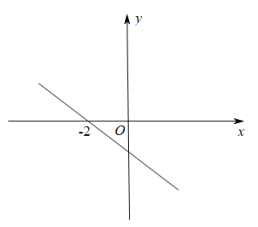14. 如图，在 $△ A B C$ 中，∠ACB=90°，∠B=15°，点D为AB中点，DE⊥AB交BC于点E，BE=8cm，则AC=cm．

查看试题解析
15. 在平面直角坐标系中，A、B两点的坐标分别为A(1，2)、B(4，1)，点P为x轴上一点，当PA+PB最小时，则点P的坐标为

查看试题解析
16. 已知一次函数y=2x+6-2a(a为常数)

(1)、若该函数图象与y轴的交点位于y轴的正半轴上，则a的取值范围是

(2)、当-1≤x≤2时，函数y有最大值-3，则a的值为

查看试题解析

三、解答题

17. 已知正比例函数图象经过点 $(- 1 ， 2)$

(1)、求此正比例函数的解析式；

(2)、点 $(2 ， - 2)$ 是否在此函数图象上？请说明理由．

查看试题解析
18. 在每个小正方形的边长为1个单位长度的网格中建立如图所示的平面直角坐标系，△ABC的顶点均在格点(网格线的交点)上．

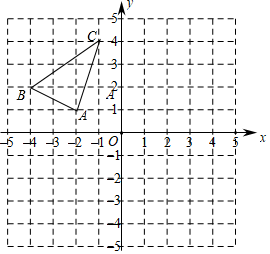
⑴画出△ABC关于y轴对称的ΔA₁B₁C₁(点A、B、C的对应点分别为点A₁、 B₁、C₁)；

⑵将(1)中得到的△A₁B₁C₁向下平移5个单位得到△A₂B₂C₂ ，画出ΔA₂B₂C₂(点A₁、B₁、 C₁的对应点分别为点A₂、B₂、 C₂)；

⑶在△ABC中有一点P(a，b)，直接写出经过以上两次图形变换后点P的对应点P₂的坐标．

查看试题解析
19. 证明：等腰三角形的两底角相等

查看试题解析
20. 直线 $l$ 与直线 $y = - 2 x + 1$ 交于点 $A (2 ， a)$ ，与直线 $y = - x + 2$ 交于点 $B (b ， 1)$

(1)、求直线 $l$ 的表达式；

(2)、求直线 $l$ 、y轴、直线 $y = 2 x + 1$ 所围成的图形的面积；

查看试题解析
21. 如图，在△ABC中，∠B=40°，∠C=70°，

(1)、用直尺和圆规按下列要求作图(保留作图痕迹，不写作法)
①作∠BAC的平分线交BC于点D；②过点A作△ABC中BC边上的高AE，垂足为点E；

(2)、在（1）的基础上，求∠DAE的度数．

查看试题解析
22. 某校计划在2022年元旦时，租用8辆客车送280名师生参加拥军爱党志愿服务活动，现有A、B两种客车，它们的载客量和租金如下表，设租用A种客车x辆，租车总费用为w元（每种车至少租1辆）．

A种客车
B种客车
载客量（人/辆）
30
40
租金（元/辆）
270
320

(1)、求出w（元）与x（辆）之间函数关系式，并直接写出自变量x的取值范围；

(2)、若学校先预支2370元用于租车，间学校预支的租车费用是否够用？请说明理由

查看试题解析
23. 如图1，线段AC上有一点B，以AB、BC为边分别在AC的同侧作等边三角形ABD、BCE，连接AE、CD交于点O，连接OB．

(1)、求证：AE=DC；

(2)、如图2，取AE的中点M，取CD的中点N，连结MN、MB、NB．求证：ΔMBN为等边三角形；

(3)、若∠EAC=a，（0°＜a＜60°），直接写出∠BOC的度数．

查看试题解析

	A种客车	B种客车
载客量（人/辆）	30	40
租金（元/辆）	270	320