安徽省合肥市庐阳区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-17 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知三角形的两边长分别为5cm和9cm,则第三边长可以是( )A、6cm B、16cm C、15cm D、4cm4. 直线上有两点 , , 且 , 则与的大小关系是( )A、 B、 C、 D、无法确定5. 下列命题中,一定是真命题的是( )A、两个锐角对应相等的两个直角三角形全等 B、角平分线上的点到这个角两边的距离相等 C、等腰三角形的高、中线、角平分线互相重合 D、有一个角是40°,且腰相等的两个等腰三角形全等6. 已知方程 的解是 ,则一次函数的图象可能是( )A、
3. 已知三角形的两边长分别为5cm和9cm,则第三边长可以是( )A、6cm B、16cm C、15cm D、4cm4. 直线上有两点 , , 且 , 则与的大小关系是( )A、 B、 C、 D、无法确定5. 下列命题中,一定是真命题的是( )A、两个锐角对应相等的两个直角三角形全等 B、角平分线上的点到这个角两边的距离相等 C、等腰三角形的高、中线、角平分线互相重合 D、有一个角是40°,且腰相等的两个等腰三角形全等6. 已知方程 的解是 ,则一次函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,点、在线段上,若 , 则添加下列条件,不一定能使的是( )
7. 如图,点、在线段上,若 , 则添加下列条件,不一定能使的是( ) A、 , B、 , C、 , D、 ,8. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , …,按这样的运动规律,经过第2022次运动后,动点的坐标是( )
A、 , B、 , C、 , D、 ,8. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , …,按这样的运动规律,经过第2022次运动后,动点的坐标是( )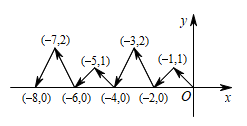 A、 B、 C、 D、9. 如图,在中,为的平分线, , 垂足为 , 且 , , , 则与的关系为( )
A、 B、 C、 D、9. 如图,在中,为的平分线, , 垂足为 , 且 , , , 则与的关系为( ) A、 B、 C、 D、10. 如图,在与中, , , , 点 , , 三点在同一条直线上,连接 , . 在以下判断中,错误的是( )
A、 B、 C、 D、10. 如图,在与中, , , , 点 , , 三点在同一条直线上,连接 , . 在以下判断中,错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数y= 中,自变量x的取值范围是 .12. 等腰三角形的一边长为5,周长为21,则该三角形的一腰长是 .13. 如图,中, , , 的垂直平分线交于 , 交于 , , 则 .
 14. 已知直线与直线在第四象限交于点 , 若直线与轴的交点为 .(1)、若点的坐标为 , 则 .(2)、的取值范围是 .
14. 已知直线与直线在第四象限交于点 , 若直线与轴的交点为 .(1)、若点的坐标为 , 则 .(2)、的取值范围是 .三、解答题
-
15. 已知一次函数的图象经过A(2,﹣3)、B(﹣1,3)两点.(1)、求这个函数的解析式;(2)、判断点P(3,﹣5)是否在该函数图象上.16. 如图,三个顶点的坐标分别为 , ,
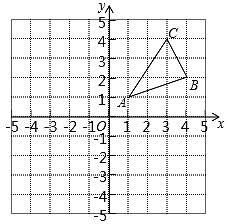
⑴请画出关于轴成轴对称的图形;
⑵在轴上找一点 , 使的值最小,请直接写出点的坐标.
17. 如图,是的角平分线, , , 求的度数. 18. 已知与成正比例,且当时, .
18. 已知与成正比例,且当时, . (1)、求与之间的函数表达式;(2)、在如图所示的平面直角坐标系中,画出函数图象;并结合图象,当时,直接写出的取值范围.19. 如图,、相交于点 , , 于点 , 于点 , 且 .
(1)、求与之间的函数表达式;(2)、在如图所示的平面直角坐标系中,画出函数图象;并结合图象,当时,直接写出的取值范围.19. 如图,、相交于点 , , 于点 , 于点 , 且 .求证: .
 20. 如图,直线的函数表达式为: , 与x轴交于点B,直线经过点 , 并与直线交于点 .
20. 如图,直线的函数表达式为: , 与x轴交于点B,直线经过点 , 并与直线交于点 .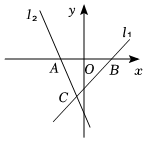 (1)、求直线的解析式;(2)、点P在直线上,点Q在直线上,轴,若 , 求点P的坐标.21. 如图1,在中, , , 于点 , 于点 .
(1)、求直线的解析式;(2)、点P在直线上,点Q在直线上,轴,若 , 求点P的坐标.21. 如图1,在中, , , 于点 , 于点 . (1)、求证:;(2)、如图2,若点O为的中点,连接DO,EO,判断的形状,并说明理由.
(1)、求证:;(2)、如图2,若点O为的中点,连接DO,EO,判断的形状,并说明理由.
