安徽省阜阳市颍东区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-17 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 小明不慎将一块三角形的玻璃打碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去.
2. 下列运算正确的是( )A、 B、 C、 D、3. 小明不慎将一块三角形的玻璃打碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去. A、第1块 B、第2块 C、第3块 D、第4块4. 三角形的两边长分别为 和 ,则周长 的范围是( )A、 B、 C、 D、5. 下列各个图形中,哪一个图形中AD是△ABC中BC边上的高( )A、
A、第1块 B、第2块 C、第3块 D、第4块4. 三角形的两边长分别为 和 ,则周长 的范围是( )A、 B、 C、 D、5. 下列各个图形中,哪一个图形中AD是△ABC中BC边上的高( )A、 B、
B、 C、
C、 D、
D、 6. 如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( )
6. 如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( ) A、95° B、125° C、130° D、135°7. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、8. 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件 件,根据题意可列方程为( )A、 B、 C、 D、9. 如图, , 点是内的定点且 , 若点M、N分别是射线OA、OB上异于点的动点,则周长的最小值是( )
A、95° B、125° C、130° D、135°7. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、8. 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件 件,根据题意可列方程为( )A、 B、 C、 D、9. 如图, , 点是内的定点且 , 若点M、N分别是射线OA、OB上异于点的动点,则周长的最小值是( ) A、3 B、 C、 D、610. 如图,在△ABC中,AB=6,AC=8,BC=10,△ABD , △ACE , △BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( )
A、3 B、 C、 D、610. 如图,在△ABC中,AB=6,AC=8,BC=10,△ABD , △ACE , △BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 当时,分式的值不存在.12. 因式分解:.13.
如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
 14. 如图,在△中, , 和的平分线交于点 , 得;和的平分线交于点 , 得;和的平分线交于点 , 则 .
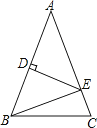
14. 如图,在△中, , 和的平分线交于点 , 得;和的平分线交于点 , 得;和的平分线交于点 , 则 . 15. 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,则∠DAE= .
15. 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,则∠DAE= .
三、解答题
-
16. 计算:;17. 已知 , , 求的值.18. 如图,已知点E,F在线段AB上, , , .求证:.
 19. 如图, , 是某个轴对称图形上的两点,且互为对称点,已知此图形上有点.
19. 如图, , 是某个轴对称图形上的两点,且互为对称点,已知此图形上有点. (1)、求点C关于该图形对称轴对称的点的坐标;(2)、求的面积20. 观察猜想:
(1)、求点C关于该图形对称轴对称的点的坐标;(2)、求的面积20. 观察猜想:如图,大长方形是由四个小长方形拼成的
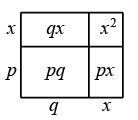 (1)、请根据此图填空:
(1)、请根据此图填空:()().
说理验证:
事实上,我们也可以用如下方法进行变形:
=()()
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用:
例题:把分解因式.
解:.
(2)、请利用上述方法将下面多项式因式分解:;21. 为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.(1)、求甲、乙两车单独运完此堆垃圾各需运多少趟?(2)、若单独租用一台车,租用哪台车合算?22. 夏夏和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中,请仔细观察下面的图形和表格,并回答下列问题:
多边形的顶点数
4
5
6
7
8
……
从一个顶点出发的对角线的条数
1
2
3
4
5
……
①____
多边形对角线的总条数
2
5
9
14
20
……
② ____
(1)、观察探究:请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①;②.(2)、拓展应用:有一个76人的代表团,由于任务需要每两人之间通1次电话(且只通1次电话),他们一共通了多少次电话?
23. 如图所示,点O是等边三角形 内一点,∠AOB=110°, ,以 为边作等边三角形 ,连接 (1)、当 =150°时,试判断 的形状,并说明理由;(2)、探究:当 为多少度时, 是以 为底的等腰三角形?
(1)、当 =150°时,试判断 的形状,并说明理由;(2)、探究:当 为多少度时, 是以 为底的等腰三角形?