安徽省池州市贵池区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-17 类型:期末考试
一、单选题
-
1. 下列平面图形中,不是轴对称图形为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列线段,能组成三角形的是( )A、2cm,3cm,5cm B、5cm,6cm,10cm C、1cm,1cm, 3cm D、3cm, 4cm, 8cm3. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、同一三角形内等角对等边 C、同角的余角相等 D、全等三角形对应角相等4. 已知点P(a,3+a)在第二象限,则a的取值范围是( )A、a<0 B、a>﹣3 C、﹣3<a<0 D、a<﹣35. 在平面直角坐标系中,已知点A(1,2)、B(2,1)、C(﹣1,﹣3)、D(﹣2,3),其中不可能与点E(1,3)在同一函数图象上的一个点是( )A、点A B、点B C、点C D、点D6. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )
2. 下列线段,能组成三角形的是( )A、2cm,3cm,5cm B、5cm,6cm,10cm C、1cm,1cm, 3cm D、3cm, 4cm, 8cm3. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、同一三角形内等角对等边 C、同角的余角相等 D、全等三角形对应角相等4. 已知点P(a,3+a)在第二象限,则a的取值范围是( )A、a<0 B、a>﹣3 C、﹣3<a<0 D、a<﹣35. 在平面直角坐标系中,已知点A(1,2)、B(2,1)、C(﹣1,﹣3)、D(﹣2,3),其中不可能与点E(1,3)在同一函数图象上的一个点是( )A、点A B、点B C、点C D、点D6. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )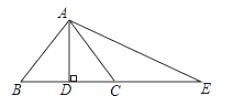 A、AB>AC=CE B、AB=AC>CE C、AB>AC>CE D、AB=AC=CE7. 如图,△ABC中,AB=AC,EB=EC,则由“SSS”直接可以判定
A、AB>AC=CE B、AB=AC>CE C、AB>AC>CE D、AB=AC=CE7. 如图,△ABC中,AB=AC,EB=EC,则由“SSS”直接可以判定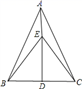 A、△ABD≌△ACD B、△ABE≌△ACE C、△BDE≌△CDE D、以上答案都不对8. 已知△ABC的两条高分别为4和12,第三条高也为整数,则第三条高所有可能值为( )A、3和4 B、1和2 C、2和3 D、4和59. 甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离 与运动时间 的函数关系大致如图所示,下列说法中错误的是( ).
A、△ABD≌△ACD B、△ABE≌△ACE C、△BDE≌△CDE D、以上答案都不对8. 已知△ABC的两条高分别为4和12,第三条高也为整数,则第三条高所有可能值为( )A、3和4 B、1和2 C、2和3 D、4和59. 甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离 与运动时间 的函数关系大致如图所示,下列说法中错误的是( ).
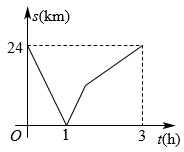 A、两人出发1小时后相遇 B、赵明阳跑步的速度为 C、王浩月到达目的地时两人相距 D、王浩月比赵明阳提前 到目的地10. 如图,已知,BD为△ABC 的角平分线,且 BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD、其中正确的有( )个.
A、两人出发1小时后相遇 B、赵明阳跑步的速度为 C、王浩月到达目的地时两人相距 D、王浩月比赵明阳提前 到目的地10. 如图,已知,BD为△ABC 的角平分线,且 BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD、其中正确的有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 函数y= 中,自变量x的取值范围是 .12. 在平面直角坐标系中有一点A(﹣2,1),将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为 .13. 已知点P(a,b)在一次函数y=2x+1的图象上,则2a﹣b= .14. 如图,函数y=2x和y=ax+b的图象相交于点A(m,3),则关于x的不等式2xax+b的最小整数解为 .
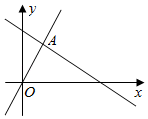 15. 如图,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是 .
15. 如图,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是 .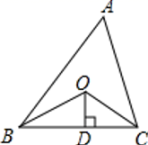 16. 等腰三角形的两边长分别为5cm和2cm,则它的周长为 .17. 如图所示,△ABC的两条中线AD,BE交于点F,连接CF,若△ABF的面积为8,则△ABC的面积为.
16. 等腰三角形的两边长分别为5cm和2cm,则它的周长为 .17. 如图所示,△ABC的两条中线AD,BE交于点F,连接CF,若△ABF的面积为8,则△ABC的面积为. 18. 如图,把 放置在平面直角坐标系中,已知 , , , ,点 在第四象限,则点 的坐标是 .
18. 如图,把 放置在平面直角坐标系中,已知 , , , ,点 在第四象限,则点 的坐标是 . 19. 如图,△ABC的顶点分别为A(0,3),B(﹣4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是.
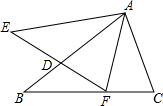
19. 如图,△ABC的顶点分别为A(0,3),B(﹣4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是. 20. 如图,与中, , , , 交于D.给出下列结论:
20. 如图,与中, , , , 交于D.给出下列结论:①;②;③;④ .
其中正确的结论是(填写所有正确结论的序号).
三、解答题
-
21. 如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2),
 (1)、请画出上述平移后的△A1B1C1 , 并写出点A、C、A1、C1的坐标;(2)、求线段AC扫过的面积.22. 如图,在 中, , 分别是 , 的角平分线.
(1)、请画出上述平移后的△A1B1C1 , 并写出点A、C、A1、C1的坐标;(2)、求线段AC扫过的面积.22. 如图,在 中, , 分别是 , 的角平分线.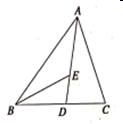 (1)、若 , ,则 的度数是;(2)、探究 与 的数量关系,并证明你的结论.23. 已知与成正比例,且当时, . 求:(1)、y与x的函数关系;(2)、当时,y的值.24. 在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为8cm.
(1)、若 , ,则 的度数是;(2)、探究 与 的数量关系,并证明你的结论.23. 已知与成正比例,且当时, . 求:(1)、y与x的函数关系;(2)、当时,y的值.24. 在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为8cm.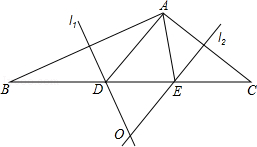 (1)、求BC的长;(2)、分别连结OA、OB、OC,若△OBC的周长为18cm,求OA的长.25. 已知,如图,延长 的各边,使得 , ,顺次连接 ,得到 为等边三角形.
(1)、求BC的长;(2)、分别连结OA、OB、OC,若△OBC的周长为18cm,求OA的长.25. 已知,如图,延长 的各边,使得 , ,顺次连接 ,得到 为等边三角形.
求证:
(1)、 ;(2)、 为等边三角形.26. 如图,直线l1 , l2交于点A , 直线l2与x轴交于点B , 与y轴交于点D , 直线l1所对应的函数关系式为y=-2x+2.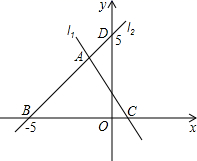 (1)、求点C的坐标及直线l2所对应的函数关系式;(2)、求△ABC的面积;(3)、在直线l2上存在一点P , 使得PB=PC , 请直接写出点P的坐标.27. 某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A,B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
(1)、求点C的坐标及直线l2所对应的函数关系式;(2)、求△ABC的面积;(3)、在直线l2上存在一点P , 使得PB=PC , 请直接写出点P的坐标.27. 某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A,B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?