安徽省亳州市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-17 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点M（﹣2，1）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 垃圾分类是将垃圾分门别类地投放，并通过分类清运和回收，使之重新变成资源．下面四个图形分别是可回收垃圾、不可回收垃圾、易腐垃圾和有害垃圾标志，在这四个图形中，轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（）

A、3cm，4cm，10cm B、8cm，9cm，17cm C、13cm，12cm，18cm D、5cm，5cm，11cm

查看试题解析
4. 一副三角板按如图所示方式叠放在一起，则图中∠ $α$ 等于（）

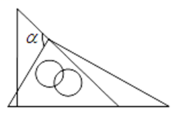A、105° B、115° C、120° D、125°

查看试题解析
5. 一次函数 $y = (k + 1) x + 3$ 的图象经过点P，且y的值随x值的增大而增大，则点P的坐标不可能为（）

A、 $(5 ， 4)$ B、 $(- 1 ， 2)$ C、 $(- 2 ， - 2)$ D、 $(5 ， - 1)$

查看试题解析
6. 已知，△ABC，△DEF，△XYZ的相关数据如图所示，则（）

A、△ABC≌△XYZ B、△DEF≌△XYZ C、 $∠ C = ∠ Z$ D、 $∠ F = 80 °$

查看试题解析
7. 在Rt△ABC中，∠C=90°，有一点D同时满足以下三个条件：①在直角边BC上；②在∠CAB的角平分线上；③在斜边AB的垂直平分线上，那么∠B为（）

A、15° B、30° C、45° D、60°

查看试题解析
8. 如图，在△MPN中，H是高MQ和NR的交点，且PM＝HN，已知MH＝3，PQ＝2，则PN的长为（）

A、5 B、7 C、8 D、11

查看试题解析
9. 定义：过△ABC的一个顶点作一条直线m，若直线m能将△ABC恰好分成两个等腰三角形，则称△ABC为“奇妙三角形”．如图，下列标有度数的四个三角形中，不是“奇妙三角形”的是（）

A、 B、 C、 D、

查看试题解析
10. 甲、乙两辆汽车沿同路线从 $A$ 地前住 $B$ 地， $A$ 、 $B$ 两地间的距离为240千米，甲车以40千米时的速度与速行驶，行驶3小时后出现故障，停车维修1小时，修好后以80千米时的速度继续行驶；乙车在甲车出发2小时后以80千米时的速度匀速前往 $B$ 地，甲、乙两车到达 $B$ 地后均作停留，下列选项中，能符合题意反映两车与 $A$ 地之同的距离 $y$ （千米）与甲车出发的时间 $x$ （小时）的函数图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 命题“直角三角形中一定有两个内角之和等于90°”的逆命题是命题．（填“真”或“假”）

查看试题解析
12. 如图，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE，如果 $A C = 4$ cm， $B C = 6$ cm，则△ACD的周长为cm．

查看试题解析
13. 在弹性限度内，弹簧的长度y cm与所挂物体的质量x kg之间是一次函数关系，其图象如图所示，则弹簧本身的长度为．

查看试题解析
14. 如图，在△ABC中，AD为中线， $A B = 6$ ．

(1)、若 $A C = 4$ ， AD长度为a，则a的取值范围为；

(2)、若 $A D ⊥ A C$ ， $∠ B A D = 30 °$ ，则AC的长度为．

查看试题解析

三、解答题

15. 已知 $△ A B C$ 为等腰三角形，请解答下列问题：

(1)、若此三角形的一个内角为 $100 °$ ，求其余两角的度数；

(2)、若该三角形两边长为2和4，求此三角形的周长．

查看试题解析
16. 如图，在平面直角坐标系中，已知 $Δ A B C$ ．

⑴将 $Δ A B C$ 向下平移6个单位，得 $Δ A_{1} B_{1} C_{1}$ ，画出 $Δ A_{1} B_{1} C_{1}$ ；

⑵画出 $Δ A_{1} B_{1} C_{1}$ 关于 $y$ 轴的对称图形 $Δ A_{2} B_{2} C_{2}$ ，并写出点 $B_{2}$ 的坐标．

（注：点 $B$ 的对应点为 $B_{1}$ ，点 $B_{1}$ 的对应点为 $B_{2}$ ）

查看试题解析
17. 学校阅览室有一种能坐4人的方桌，如果多于4人，就把方桌按图中的方式摆放，2张方桌摆放到一起能坐6人，请你结合这个规律，回答问题：

(1)、写出总人数y（人）与方桌数x（张）之间的函数解析式（不要求写自变量的取值范围），并判断y是不是x的一次函数；

(2)、若八年级（1）班有42人去阅览室看书，则需要多少张这样的方桌？

查看试题解析
18. 如图，在△ABD和△ACD中，已知AB=AC，∠B=∠C，求证：AD是∠BAC的平分线．

查看试题解析
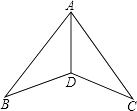19. 在两个不全等的三角形中，有两组边对应相等，其中一组是公共边，另一组等边所对的角对应相等，就称这两个三角形为共边偏差三角形．如图1，AB是公共边， $B C = B D$ ， $∠ A = ∠ A$ ．则△ABC与△ABD是共边偏差三角形．

(1)、如图2，在线段AD上找一点E，连接CE，使得△ACE与△ACD是共边偏差三角形，并简要说明理由；

(2)、在图2中，已知 $∠ 1 = ∠ 2$ ， $∠ B + ∠ D = 180 °$ ，求证：△ACB与△ACD是共边偏差三角形．

查看试题解析
20. 直线 $l_{1} ：$ y=2x－2与x轴交于点D，直线 $l_{2} ：$ y=kx+b与x轴交于点A，且经过B(3，1)，两直线相交于点C(m，2).

(1)、求直线 $l_{2}$ 的解析式和点C的坐标.

(2)、求当x取何值，kx+b≥2x－2

(3)、△ADC的面积.

查看试题解析
21. 如图，已知四个关系式：①AC＝DC；②BC＝EC；③∠DCA＝∠ECB：④AB＝DE．

(1)、从上面四个关系式中任取三个为条件，余下的一个为结论，组成一个命题．在组成的命题中真命题的个数是；

(2)、从（1）中选择一个真命题进行证明
已知：      ▲ ．
求证：      ▲ ．
证明：      ▲ ．

查看试题解析
22. 某学校计划购进A，B两种品牌的足球共50个，其中A品牌足球的价格为100元/个，购买B品牌足球所需费用y（单位：元）与购买数量x（单位：个）之间的关系如图所示

(1)、请直接写出y与x之间的函数解析式；

(2)、若购买B种品牌足球的数量不超过30个，但不少于A种品牌足球的数量，请设计购买方案，使购买总费用W（单位：元）最低，并求出最低费用.

查看试题解析
23. 在△ABC和△AED中，AC交DE于点O， $∠ B A C = ∠ E A D$ ， $A B = A C$ ， $A E = A D$ ，连接BE，CD．

(1)、如图1，求证： $B E = C D$ ；
      图1

(2)、如图2，延长DE交BC于点F，若 $∠ B E F = ∠ C D F$ ，求∠AEB的度数；
       图2

(3)、如图3，在（2）的条件下，当 $A D = B E$ 时，过点C作 $C P ⊥ B C$ 交DF于点P，若 $B F = 4$ ，求△FCP的面积．
      图3

查看试题解析