安徽省蚌埠市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-17 类型:期末考试
一、单选题
-
1. 下列微信表情是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点A(﹣3,4)离y轴的距离是( )A、3 B、4 C、5 D、73. 下列长度的三条线段不能组成三角形的是( )A、3cm,4cm,5cm B、6cm,10cm,8cm C、2cm,3cm,6cm D、2cm,2cm,3cm4. 下列命题是真命题的是( )A、如果a+b=0,那么a=b=0 B、如果ab<0,那么a<0,b>0 C、如果|a|=|b|,那么a=b D、如果直线a∥b,b∥c,那么直线a∥c5. 如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,2)黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是( )
2. 点A(﹣3,4)离y轴的距离是( )A、3 B、4 C、5 D、73. 下列长度的三条线段不能组成三角形的是( )A、3cm,4cm,5cm B、6cm,10cm,8cm C、2cm,3cm,6cm D、2cm,2cm,3cm4. 下列命题是真命题的是( )A、如果a+b=0,那么a=b=0 B、如果ab<0,那么a<0,b>0 C、如果|a|=|b|,那么a=b D、如果直线a∥b,b∥c,那么直线a∥c5. 如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,2)黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是( ) A、(2,2) B、(0,1) C、(2,﹣1) D、(2,1)6. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、(2,2) B、(0,1) C、(2,﹣1) D、(2,1)6. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )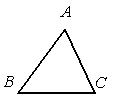 A、
A、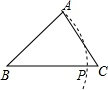 B、
B、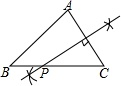 C、
C、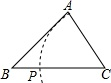 D、
D、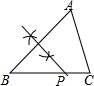 7. 对于一次函数y=-x+2,下列说法错误的是( )A、函数的图象向下平移2个单位长度得到y=-x的图象 B、函数的图象与x轴的交点坐标是(2,0) C、函数的图象不经过第三象限 D、若两点A(1,y1),B(3,y2)在该函数图象上,则y1<y28. 已知直线l1:y=kx+b与直线l2:y=-2x+4交于点C(m,2),则方程组的解是( )A、 B、 C、 D、9. 已知:如图,在 RtΔABC中,∠C = 90°,BE平分∠ABC,ED垂直平分AB,D为垂足,若AC=12,则AE的长度为( )
7. 对于一次函数y=-x+2,下列说法错误的是( )A、函数的图象向下平移2个单位长度得到y=-x的图象 B、函数的图象与x轴的交点坐标是(2,0) C、函数的图象不经过第三象限 D、若两点A(1,y1),B(3,y2)在该函数图象上,则y1<y28. 已知直线l1:y=kx+b与直线l2:y=-2x+4交于点C(m,2),则方程组的解是( )A、 B、 C、 D、9. 已知:如图,在 RtΔABC中,∠C = 90°,BE平分∠ABC,ED垂直平分AB,D为垂足,若AC=12,则AE的长度为( ) A、4 B、5 C、6 D、810. 已知:如图,在等边△ABC中,点D是边BC上的一个动点(不与两端点重合),连接AD,作线段AD的垂直平分线EF,分别交AB,AC于点E,F,连接ED、FD,则以下结论正确的是( )
A、4 B、5 C、6 D、810. 已知:如图,在等边△ABC中,点D是边BC上的一个动点(不与两端点重合),连接AD,作线段AD的垂直平分线EF,分别交AB,AC于点E,F,连接ED、FD,则以下结论正确的是( ) A、∠1 =15° B、DF⊥AC C、CD=2CF D、∠2=2∠1
A、∠1 =15° B、DF⊥AC C、CD=2CF D、∠2=2∠1二、填空题
-
11. 函数y= 中,自变量x的取值范围是 .12. 在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则估计口袋中白球大约有个.13. 已知点P(3,y1),Q(-2,y2)在一次函数y =(2m-1)x+2的图象上,且y1<y2 , 则m 的取值范围是 .14. 如图,在△ABC中, , ,AD是△ABC的中线,AE是∠BAD的角平分线,DF//AB交AE的延长线于点F,则DF的长为.

三、解答题
-
15. 已知:如图,A1 , A2 , A3是∠MON的ON边上顺次三个不同的点,B1 , B2 , B3是∠MON的OM边上顺次三个不同的点,且有OA1=A1B1=B1A2=A2B2=B2A3
 (1)、当∠MB1A2=45°时,∠MON =;(2)、若OM边上不存在B3点,使得A3B3=B2A3 , 则∠MON的最小值是 .16. 已知:如图,在平面直角坐标系中,已知A(1,4)、B(3,1)、C(3、5).
(1)、当∠MB1A2=45°时,∠MON =;(2)、若OM边上不存在B3点,使得A3B3=B2A3 , 则∠MON的最小值是 .16. 已知:如图,在平面直角坐标系中,已知A(1,4)、B(3,1)、C(3、5). (1)、点A先向右平移3个单位,再向下平移2个单位,所得点的坐标为;(2)、画出△ABC关于y轴对称的△A1B1C1;(3)、已知点D的横纵坐标都是整数,且△BCD和△BCA全等,请直接写出一个满足条件的点D的坐标为 . (D不与A重合).17. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取点M、N,使得OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线.
(1)、点A先向右平移3个单位,再向下平移2个单位,所得点的坐标为;(2)、画出△ABC关于y轴对称的△A1B1C1;(3)、已知点D的横纵坐标都是整数,且△BCD和△BCA全等,请直接写出一个满足条件的点D的坐标为 . (D不与A重合).17. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取点M、N,使得OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线. (1)、求证:OC平分∠AOB;(2)、已知∠AMC=40°,∠MCN=30°,求∠AOB的度数;18. 直线 y=2x-2与x轴交于点D,直线 y=kx+b与x轴交于点A,且经过B(3,1),两直线相交于点C(m,2).
(1)、求证:OC平分∠AOB;(2)、已知∠AMC=40°,∠MCN=30°,求∠AOB的度数;18. 直线 y=2x-2与x轴交于点D,直线 y=kx+b与x轴交于点A,且经过B(3,1),两直线相交于点C(m,2). (1)、求直线 的解析式和点C的坐标.(2)、求当x取何值,kx+b≥2x-2(3)、△ADC的面积.19. 小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好
(1)、求直线 的解析式和点C的坐标.(2)、求当x取何值,kx+b≥2x-2(3)、△ADC的面积.19. 小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好 (1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是.(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)20. 某水果超市欲购进甲,乙两种水果进行销售.甲种水果每千克的价格为a元,如果一次购买超过40千克,超过部分的价格打八折,乙种水果的价格为26元/千克.设水果超市购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.
(1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是.(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)20. 某水果超市欲购进甲,乙两种水果进行销售.甲种水果每千克的价格为a元,如果一次购买超过40千克,超过部分的价格打八折,乙种水果的价格为26元/千克.设水果超市购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示. (1)、a=(2)、求y与x之间的函数关系式;(3)、若经销商计划一次性购进甲,乙两种水果共80千克,且甲种水果不少于30千克,但又不超过50千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额W(元)最少?21. 已知△ABC与ΔADE均为等腰直角三角形,且∠BAC=∠DAE=90°,点D在直线BC上.
(1)、a=(2)、求y与x之间的函数关系式;(3)、若经销商计划一次性购进甲,乙两种水果共80千克,且甲种水果不少于30千克,但又不超过50千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额W(元)最少?21. 已知△ABC与ΔADE均为等腰直角三角形,且∠BAC=∠DAE=90°,点D在直线BC上. (1)、如图1,当点D在CB延长线上时,求证:BE⊥CD;(2)、如图2,当D点不在直线BC上时, BE、CD相交于M,
(1)、如图1,当点D在CB延长线上时,求证:BE⊥CD;(2)、如图2,当D点不在直线BC上时, BE、CD相交于M,①直接写出∠CME的度数;
②求证:MA平分∠CME