四川省雅安市重点高中2022-2023学年高一上学期9月开学测试数学试题
试卷更新日期:2022-10-17 类型:开学考试
一、单选题(每小题5分,共6题,共60分.)
-
1. 不等式 的解集为( )A、 或 B、 C、 或 D、2. 将分解因式,所得结果正确的是( )A、 B、 C、 D、3. 方程组的解组成的集合为( )A、 B、或 C、 , D、4. 关于x的不等式的解集为( )A、 B、 C、 D、5. 已知集合 , 若.则实数a的值为( )A、1 B、1或 C、 D、或6. 如果集合 中只有一个元素,则a的值是( )A、0 B、-1 C、0或1 D、0或-17. 若集合 , , 则( )A、 B、 C、 D、8. 已知集合 , .若 , 则实数m的取值范围为( )A、 B、 C、 D、9. 函数的值域( )A、 B、 C、 D、10. 关于x的一元二次方程有两个实数根 , , 则代数式写的最小值是( )A、-8 B、-5 C、1 D、211. 已知全集 , 集合 , , 则图中阴影部分表示的集合为( )
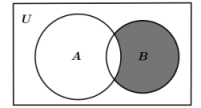 A、 B、 C、 D、12. 设集合 , .则( )A、 B、 C、 D、
A、 B、 C、 D、12. 设集合 , .则( )A、 B、 C、 D、二、填空题(每题5分,共4题,共20分)
-
13. 因式分解:.14. 已知 , 则的值等于.15. 已知 , , , 则代数式的值为.16. 已知函数 在区间 上不单调,则实数a的取值范围是.
三、简答题(共6小题,共70分)
-
17.(1)、解不等式;(2)、已知方程有一个根,求整数m的值.18. 已知集合 , 集合.(1)、当时,求;(2)、若 , 求实数m的取值范围19. 设 , , ,(1)、分别求 ,(2)、若 , 求实数a的取值范围.