备考2023年中考数学杭州卷变式阶梯训练21-23题

试卷更新日期：2022-10-16 类型：二轮复习

进入出卷网下载

一、第二十一题

1. 如图，在Rt△ACB中，∠ACB=90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A=50°，∠ACE=30°．

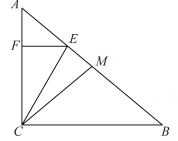(1)、求证：CE=CM.

(2)、若AB=4，求线段FC的长.

查看试题解析
2. 在△ABC中，∠C＝90°.

(1)、已知c＝8 $\sqrt{3}$ ， ∠A＝60°，求∠B，a，b；

(2)、已知a＝3 $\sqrt{6}$ ， ∠A＝45°，求∠B，b，c.

查看试题解析
3. 已知：如图，AO是⊙O的半径，AC为⊙O的弦，点F为的中点，OF交AC于点E，AC=10，EF=3·

(1)、求AO的长；

(2)、过点C作CD⊥AO，交AO延长线于点D，求OD的长·

查看试题解析
4. 如图，在Rt $△$ ABC中， $∠ B A C = 90 °$ ，点O为BC上一点，以O为圆心、OB为半径的⊙ $O$ 切AC于点D，连接OA、BD、OA与BD相交于点E.

(1)、求证：BD平分 $∠ A B C$ ；

(2)、若 $∠ C = 30 °$ ， ⊙ $O$ 的半径为10，求OE的长.

查看试题解析
5. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， ∠A，∠B，∠C所对的边分别是a，b，c，利用锐角三角函数定义很容易推导出一些关系式，如 $s i n^{2} A + c o s^{2} A = 1$ ， $s i n A = c o s B$ 等，这些公式在三角函数式子的变形中运用比较广泛．设 $α$ ， $β$ 是锐角，定义：当 $α > β$ 时，两角和的余弦公式： $c o s (α + β) = c o s α c o s β - s i n α s i n β$ ．
例：计算 $c o s 75 °$ 的值．
$c o s 75 ° = c o s (45 ° + 30 °) = c o s 45 ° c o s 30 ° - s i n 45 ° s i n 30 °$
$= \frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} \times \frac{1}{2}$ $= \frac{\sqrt{6}}{4} - \frac{\sqrt{2}}{4}$ $= \frac{\sqrt{6} - \sqrt{2}}{4}$ ，
两角差的余弦公式： $c o s (α - β) = c o s α c o s β + s i n α s i n β$ ．利用类比的方法运用公式求解．

(1)、计算 $c o s 15 ° =$ ．

(2)、计算 $c o s 80 ° c o s 35 ° + s i n 80 ° s i n 35 °$ 的值；

(3)、一副斜边长均为16的三角板拼成如图所示的图形，求过A、B、C、D四点的矩形ABEF的面积．

查看试题解析
6.

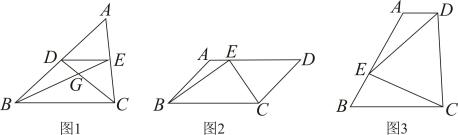(1)、问题提出：如图1，在 $△ A B C$ 中，点 $D$ 、 $E$ 分别是 $A B$ 、 $A C$ 的中点，连接 $D E$ 、 $C D$ 、 $B E$ ， $C D$ 与 $B E$ 交于点 $G$ ，若 $S_{△ D E G} = 2$ ，则 $S_{△ B C G} =$ ；

(2)、问题探究：如图2，在 $▱ A B C D$ 中， $A B = 2$ ， $∠ D = 45 °$ ，点 $E$ 是 $A D$ 上一点（可与端点重合），连接 $B E$ 、 $C E$ ， $B E ⊥ C E$ ，求 $▱ A B C D$ 面积的最小值；

(3)、问题解决：某湿地公园拟建一个梯形花园 $A B C D$ ，示意图如图3所示，其中 $A D ∥ B C$ ， $A B = 60 \sqrt{3} m$ ， $∠ A B C = 60 °$ .管理员计划在 $△ A D E$ 区域种植水生植物，在 $△ A D E$ 区域种植甲种花卉.根据设计要求，要满足点 $E$ 在 $A B$ 上， $A E = 2 B E$ ， $∠ D E C$ 是锐角，且 $t a n ∠ D E C = 2$ ，若种植水生植物每平方米需400元，种植甲种花卉每平方米需100元，求种植水生植物和种植甲种花卉所需总费用至少为多少元？

查看试题解析
7. 如图，矩形ABCD中，AB=6，BC=2 $\sqrt{3}$ ，点O是AB的中点，点P在AB的延长线上，且BP=3.一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒（t≥0）.

(1)、当等边△EFG的边FG恰好经过点C时，求运动时间t的值；

(2)、在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；

(3)、设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存大，求出对应的t的值；若不存在，请说明理由.

查看试题解析

二、第二十二题

8. 设二次函数y₁=2x²+bx+c(b，c是常数)的图象与x轴交于A，B两点．

(1)、若A，B两点的坐标分别为(1，0)，(2，0)，求函数y)的表达式及其图象的对称轴．

(2)、若函数y₁的表达式可以写成心=2(x-h)²-2(h是常数)的形式，求b+c的最小值．

(3)、设一次函数y₂=x-m(m是常数)，若函数y₁的表达式还可以写成y₁=2(x-m)(x-m-2)的形式，当函数y=y₁-y₂的图象经过点(x₀ ， 0)时，求x₀-m的值．

查看试题解析
9. 已知二次函数y＝ax²＋bx－3（a≠0）.

(1)、若函数图象的对称轴为直线x＝1，且顶点在x轴上，求a的值；

(2)、若a＝1，b＝2，点（m，n）为该二次函数图象在第三象限内的点，请分别求出m，n的取值范围；

(3)、若点P（a，a－3）始终是函数图象上的点，求证： $a^{2} + b^{2} \geq \frac{3}{4}$ .

查看试题解析
10. 如图，在平面直角坐标系中，二次函数y＝ax²+4x﹣3图象的顶点是A，与x轴交于B，C两点，与y轴交于点D.点B的坐标是（1，0）.

(1)、求A，C两点的坐标，并根据图象直接写出当y＞0时x的取值范围.

(2)、将图象向上平移m个单位后，二次函数图象与x轴交于E，F两点，若EF＝6，求m的值.

查看试题解析
11. 在直角坐标系中，点A(1，m)和点B(3，n)在二次函数 $y = a x^{2} + b x + 1 (a \neq 0)$ 的图象上.

(1)、若 $m = 1$ ， $n = 4$ ，求二次函数的表达式及图象的对称轴.

(2)、若 $m - n = \frac{1}{2}$ ，试说明二次函数的图象与x轴必有交点.

(3)、若点C( $x_{0}$ ， $y_{0}$ )是二次函数图象上的任意一点，且满足 $y_{0} \leq m$ ，求mn的取值范围.

查看试题解析
12. 平面直角坐标系 $x O y$ 中，已知抛物线 $y = x^{2} + b x + c$ 经过 $(- 1 ， m^{2} + 2 m + 1)$ ， $(0 ， m^{2} + 2 m + 2)$ 两点，其中 $m$ 为常数．

(1)、求 $b$ 的值，并用含 $m$ 的代数式表示 $c$ ；

(2)、若抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴有公共点，求 $m$ 的值；

(3)、设 $(a ， y_{1})$ ， $(a + 2 ， y_{2})$ 是抛物线 $y = x^{2} + b x + c$ 上的两点，请比较 $y_{2} - y_{1}$ 与0的大小，并说明理由．

查看试题解析
13. 在平面直角坐标系中，抛物线L：y＝﹣x²+x+2与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧）.

(1)、求A、B、C三点的坐标；

(2)、连接AC、BC，以点C为位似中心，将△ABC扩大到原来的2倍得到△A₁B₁C，其中点A₁、B₁分别是点A、B的对应点，如何平移抛物线L才能使其同时经过点A₁、B₁ ，求出所有的平移方式.

查看试题解析
14. 定义：若两条抛物线在x轴上经过两个相同点，那么我们称这两条抛物线是“同交点抛物线”，在x轴上经过的两个相同点称为“同交点”，已知抛物线y=x² +bx+c经过(﹣2，0)、( ﹣4，0)，且一条与它是“同交点抛物线”的抛物线y=ax² +ex+f经过点( ﹣3，3)．

(1)、求b、c及a的值；

(2)、已知抛物线y =﹣x² +2x +3与抛物线y_n= $\frac{n}{3}$ x²﹣ $\frac{2 n}{3}$ x﹣n （n为正整数）
①抛物线y和抛物线y_n是不是“同交点抛物线”？若是，请求出它们的“同交点”，并写出它们一条相同的图像性质；若不是，请说明理由．

②当直线y = $\frac{1}{2}$ x+ m与抛物线y、y_n ，相交共有4个交点时，求m的取值范围．

③若直线y =k（k <0）与抛物线y =﹣x² +2x +3与抛物线y_n = $\frac{n}{3}$ x²﹣ $\frac{2 n}{3}$ x﹣n （n为正整数）共有4个交点，从左至右依次标记为点A、点B、点C、点D，当AB =BC=CD时，求出k、n之间的关系式

查看试题解析

三、第二十三题

15. 在正方形ABCD中，点M是边AB的中点，点E在线段AM上（不与点A重合），点F在边BC上，且AE=2BF，连接EF，以EF为边在正方形ABCD内作正方形EFGH．

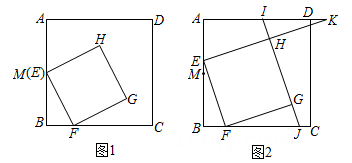(1)、如图1．若AB=4，当点E与点M重合时，求正方形EFGH的面积

(2)、如图2．已知直线HG分别与边AD，BC交于点I，J，射线EH与射线AD交于点K．
①求证：EK=2EH；

②设∠AEK=α，△FGJ和四边形AEHI的面积分别为S₁、S₂ ．

求证： $\frac{S_{2}}{S_{1}}$ =4sin²α-1．

查看试题解析
16. 如图，点 $E$ ， $F$ 分别在正方形 $A B C D$ 的边 $A B$ ， $A D$ 上，且 $A E = D F$ ，点 $G$ ， $H$ 分别在边 $A B$ ， $B C$ 上，且 $F G ⊥ E H$ ，垂足为 $P$ ．

(1)、求证： $F G = E H$ ；

(2)、若正方形 $A B C D$ 边长为5， $A E = 2$ ， $t a n ∠ A G F = \frac{3}{4}$ ，求 $P F$ 的长度．

查看试题解析
17. 如图，对折正方形纸片 $A B C D$ ，使 $A B$ 与 $D C$ 重合，折痕为 $M N$ .将纸片展平，再进行折叠，使点C落在 $M N$ 上的点E处，折痕 $B P$ 交 $M N$ 于点F.

(1)、求证： $E F = P C$ ；

(2)、若正方形纸片 $A B C D$ 的边长为3，求折痕 $B P$ 的长.

查看试题解析
18. 如图①，四边形 $A B C D$ 是正方形，点E是 $B C$ 上一点，连接 $A E$ ，以 $A E$ 为一边作正方形 $A E F G$ ，连接 $D G$ ．

(1)、求证： $D G = B E$ ；

(2)、如图②，连接 $A F$ 交 $C D$ 于点H，连接 $E H$ ，求证： $E H = B E + D H$ ；

(3)、在（2）的条件下，若 $A B = 4$ ，点H恰为 $C D$ 中点，求 $△ C E H$ 的面积．

查看试题解析
19. 正方形 $A B C D$ 边长为3，点 $E$ 是 $C D$ 上一点，连接 $B E$ 交 $A C$ 于点 $F$ .

(1)、如图1，若 $C E = 1$ ，求 $C F$ 的值；

(2)、如图1，若 $S_{△ C B F} = \frac{3}{2}$ ，求证：点 $E$ 是 $C D$ 的中点；

(3)、如图2，点 $G$ 为 $B C$ 上一点，且满足 $∠ G A C = ∠ E B C$ ，设 $C E = x$ ， $G B = y$ ，试探究 $y$ 与 $x$ 的函数关系.

查看试题解析
20. 如图
如图（1），在Rt△ABC中，∠C＝90°，边AC＝8，BC＝6，点M、N分别在线段AC、BC上，将△ABC沿直线MN翻折，点C的对应点是C′．

(1)、当M、N分别是所在边的中点时，求线段CC′的长度；

(2)、若CN＝2，求点C′到线段AB的最短距离；

(3)、如图（2），当点C′落在边AB上时，
①四边形CMC′N能否成为正方形？若能，求出CM的值；若不能，说明理由．
②请直接写出点C′运动的路程长度．

查看试题解析
21. 【探索发现】
如图①，将△ABC沿中位线EH折叠，使点A的对称点D落在BC边上，再将△BED和△DHC分别沿EF、HG折叠，使点B、C均落在点D处，折痕形成一个四边形EFGH.小刚在探索这个问题时发现四边形EFGH是矩形.

小刚是这样想的：

(1)、请参考小刚的思路写出证明过程；

(2)、连接AD，当AD＝BC时，直接写出线段EF，BF，CG的数量关系；

(3)、【理解运用】
如图②，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8，DC＝10，AD＜BC，点E为AB的中点，把四边形ABCD折叠成如图②所示的正方形EFGH，顶点C，D落在点M处，顶点A，B落在点N处，求BC的长.

查看试题解析