备考2023年中考数学杭州卷变式阶梯训练17--20题

试卷更新日期：2022-10-16 类型：二轮复习

进入出卷网下载

一、第十七题

1. 计算：(-6) ×( $\frac{2}{3}$ -■)-2³ ．
圆圆在做作业时，发现题中有一个数字被墨水污染了。

(1)、如果被污染的数字是 $\frac{1}{2}$ ．请计算(-6)×( $\frac{2}{3}$ - $\frac{1}{2}$ )-2³ ．

(2)、如果计算结果等于6，求被污染的数字．

查看试题解析
2. 嘉淇在解一道数学计算题时，发现有一个数被污染了．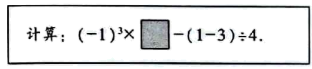

(1)、嘉淇猜污染的数为1，请计算 ${(- 1)}^{3} \times 1 - (1 - 3) \div 4$ ；

(2)、老师说，嘉淇猜错了，正确的计算结果不小于 $\frac{5}{2}$ ，求被污染的数最大是几？

查看试题解析
3. 某同学在解关于y的方程 $\frac{3 y - a}{4} - \frac{5 y - 7 a}{6} =$ 1去分母时、忘记将方程右边的1乘以12，从而求得方程的解为y＝10．

(1)、求a的值；

(2)、求方程正确的解．

查看试题解析
4. 张老师在电脑上设计了一个有理数运算程序：输入a，加*键，再输入b，得到运算：a*b＝a²－b²－[2（a³－1）－ $\frac{1}{b}$ ]÷（a＋b）.

(1)、求（－2）* $\frac{1}{2}$ 的值；

(2)、张老师随机输入了一组数据，运用此程序进行计算时，屏幕上显示“该程序无法操作”这说明了输入的数据可能出现了什么情况？为什么？

查看试题解析
5. 洪洪同学在电脑中设置了一个有理数的运算程序：输入数“a”加“★”键再输入“b”，就可以得到运算 $a ★ b = | 2 - a^{2} | - \frac{1}{b} + 1$ ．

(1)、按此程序 $(- 3) ★ 2 =$ ；

(2)、若淇淇输入数“-1”加“★”键再输入“x”后，电脑输出的数为1，求x的值；

(3)、嘉嘉同学运用淇淇设置的在这个程序时，屏幕显示：“该操作无法进行，”你能说出嘉嘉在什么地方出错了吗？

查看试题解析
6. 一般情况下 $\frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3}$ 不成立，但有些数可以使得它成立，例如：a＝b＝0，我们称使得 $\frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3}$ 成立的一对数a，b为“双语数对”，记为（a，b）.

(1)、填空：（－4，9）“双语数对”（填“是”或“否”）；

(2)、若（1，b）是“双语数对”，求b的值；

(3)、已知（m，n）是“双语数对”，试说明 $(m + 1 ， n - \frac{9}{4})$ 也是“双语数对”.

查看试题解析
7. 对于一个数x，我们用 $(x]$ 表示小于x的最大整数，例如： $(2.6] = 2$ ， $(- 3] = - 4$ .

(1)、填空： $(10] =$ ， $(- 2019] =$ ， $(\frac{1}{7}] =$ ；

(2)、若a，b都是整数，且 $(a]$ 和 $(b]$ 互为相反数，求代数式 $a - (a + b) \times 3 + b$ 的值；

(3)、若 $| (x] | + | (x - 2] | = 6$ ，求x的取值范围.

查看试题解析

二、第十八题

8. 某校学生会要在甲、乙两位候选人中选择一人担任文艺部干事，对他们进行了文化水平、艺术水平、组织能力的测试，根据综合成绩择优录取．他们的各项成绩（单项满分100分）如下表所示：

候选人	文化水平	艺术水平	组织能力
甲	80分	87分	82分
乙	80分	96分	76分

(1)、如果把各项成绩的平均数作为综合成绩，应该录取谁？

(2)、如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照20%，20%，60%的比例计入综合成绩，应该录取谁？

查看试题解析

9. 某网络公司招聘一名高级网络工程师，应聘者小魏参加笔试和面试，成绩（100分制）如表所示：

	笔试	面试
成绩	98	评委1	评委2	评委3	评委4	评委5	评委6	评委7
成绩	98	94	94	93	98	98	98	96

其中规定：面试得分中去掉一个最高分和一个最低分，余下的面试得分的平均值作为应聘者的面试成绩.

(1)、请计算小魏的面试成绩；

(2)、如果面试成绩与笔试成绩按6：4的比例确定，请计算出小魏的最终成绩.

查看试题解析

10. 某学校在一次广播操比赛中，901班，902班，903班的各项得分如表：

班级	服装统一	动作整齐	动作准确
901班	85	70	85
902班	75	85	80
903班	90	85	95

(1)、若取三个项目的得分平均分作为该班成绩，分别求各班的成绩.

(2)、若学校认为三个项目的重要程度各不相同，从低到高依次为“服装统一”“动作整齐”“动作准确”，它们在总分中所占的比例分别为10％，

a

％，

b

％.请你设计一组符合要求的

a

，

b

值，并直接给出三个班级的排名顺序.

查看试题解析

11. 某公司要在甲、乙两人中招聘一名职员，对两人的学历，能力、经验这三项进行了测试．各项满分均为10分，成绩高者被录用．图1是甲、乙测试成绩的条形统计图，

(1)、分别求出甲、乙三项成绩之和，并指出会录用谁；

(2)、若将甲、乙的三项测试成绩，按照扇形统计图（图2）各项所占之比，分别计算两人各自的综合成绩，并判断是否会改变（1）的录用结果．

查看试题解析

12. 某公司要招聘一名职员，面试中甲、乙、丙三名应聘者各项得分如下表：

	学历	能力	态度
甲	80	87	85
乙	75	91	83
丙	90	78	87

(1)、若根据三项得分的平均分择优录取，已求甲的平均分为84分，通过计算确定谁将被录用？

(2)、若该公司规定学历、能力、态度测试占总分的比例分别为20%，

m %

，

n %

．若你是这家公司的招聘者，按你认为的“重要程度”设计能力和态度两项得分在总分中的比例，并以此为依据确定谁将被录用？请简要说明这样设计的理由．

查看试题解析

13. 为了分析某节复习课的教学效果，上课前，张老师让901班每位同学做6道题目 $($ 与这节课内容相关 $)$ ，解题情况如图所示：上课后，再让学生做6道类似的题目，结果如表所示．已知每位学生至少答对1题．
上课后解题情况频数统计表
答对题数
频数 $($ 人 $)$
1
2
2
3
3
3
4
10
5
9
6
13

(1)、901班有多少名学生？

(2)、该班上课前解题时答对题数的中位数是多少？

(3)、请选择适当的统计量，从两个不同的角度评价这节复习课的教学效果．

查看试题解析
14. 第19届亚运会将于2022年9月在浙江杭州举行，为了让更多的同学了解亚运会，某校甲、乙两个班级开展“亚运会知识竞答”活动.现将各班竞答成绩分为 $A$ ， $B$ ， $C$ ， $D$ 四组，依次对应优秀、良好、中等、合格四个等级，分别赋分为：10分，8分，6分，4分，并制作如下频数分布表和扇形统计图.已知乙班参赛人数为40人.
甲班知识竞答成绩频数分布表
组别
频数（人）
$A$
4
$B$
15
$C$
6
$D$
5
乙班知识竞答成绩扇形统计图

(1)、请分别求出甲、乙两个班级竞答成绩的平均分.

(2)、根据平均数、中位数、众数及成绩等级分析，你认为哪个班级成绩较好？请简述理由.

查看试题解析

三、第十九题

15. 如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，连接DE，EF．已知四边形BFED是平行四边形， $\frac{D E}{B C} = \frac{1}{4}$ 、

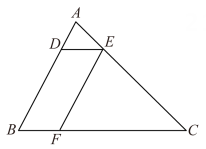(1)、若AB=8，求线段AD的长．

(2)、若△ADE的面积为1，求平行四边形BFED的面积．

查看试题解析
16. 如图， $∠ B A D = ∠ C A E$ ， $∠ B = ∠ D$ .

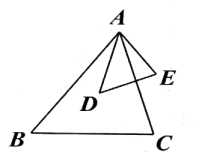(1)、 $△ A B C$ 与 $△ A D E$ 相似吗？为什么？

(2)、如果 $A B = 2 A D$ ， $B C = 4$ ，那么 $D E$ 的长为多少？

查看试题解析
17. 已知：如图，在平行四边形ABCD中，AC、DB交于点E，点F在BC的延长线上，连结EF、DF，且∠DEF=∠ADC．

(1)、求证： $\frac{E F}{B F} = \frac{A B}{D B}$ ；

(2)、如果 $B D^{2} = 2 A D \cdot D F$ ，求证：平行四边形ABCD是矩形．

查看试题解析
18. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点 $G$ ．点 $F$ 是 $C G$ 的中点，连接 $A F$ 并延长交 $⊙ O$ 于点 $E$ ，连接 $A D$ ， $D E$ ．

(1)、求证： $A D^{2} = A E \cdot A F$ ；

(2)、若 $C F = 2$ ， $A F = 3$ ，求 $△ D E F$ 的面积．

查看试题解析
19. [探索发现]
如图①，将△ABC沿中位线Eh折叠，使点A的对称点D落在BC边上，再将△BED和△DHC分别沿EF、HG折叠，使点B、C均落在点D处，折痕形成一个四边形EFGH．

(1)、求证：四边形EFGH是矩形；

(2)、连接AD，当AD=BC时，直接写出线段EF、BF、CG的数量关系，并说明理由；

(3)、如图②，在四边形ABCD中，AD∥BC，∠B=90°，AB=8，DC=10，AD<BC，点E为AB的中点，把四边形ABCD折叠成如图②所示的正方形EFGH，顶点C、D落在点M处，顶点A、B落在点N处，直接写出BC的长．

查看试题解析
20. 如图，在矩形ABCD中，对角线AC、BD相交于点O，过点D作 $D E ⊥ A C$ 于点E，作点E关于AD的对称点F，连接AF，FD，延长FD交BC的延长线于点N，交AC的延长线于点M．

(1)、判断AF与BD的位置关系并证明；

(2)、求证： $B C \cdot C N = D E \cdot D N$ ；

(3)、若 $\frac{D F}{D N} = \frac{3}{4}$ ，求 $\frac{C M}{M D}$ 的值．

查看试题解析
21.

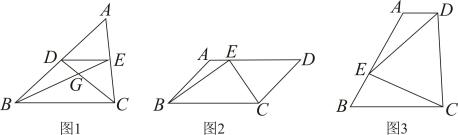(1)、问题提出：如图1，在 $△ A B C$ 中，点 $D$ 、 $E$ 分别是 $A B$ 、 $A C$ 的中点，连接 $D E$ 、 $C D$ 、 $B E$ ， $C D$ 与 $B E$ 交于点 $G$ ，若 $S_{△ D E G} = 2$ ，则 $S_{△ B C G} =$ ；

(2)、问题探究：如图2，在 $▱ A B C D$ 中， $A B = 2$ ， $∠ D = 45 °$ ，点 $E$ 是 $A D$ 上一点（可与端点重合），连接 $B E$ 、 $C E$ ， $B E ⊥ C E$ ，求 $▱ A B C D$ 面积的最小值；

(3)、问题解决：某湿地公园拟建一个梯形花园 $A B C D$ ，示意图如图3所示，其中 $A D ∥ B C$ ， $A B = 60 \sqrt{3} m$ ， $∠ A B C = 60 °$ .管理员计划在 $△ A D E$ 区域种植水生植物，在 $△ A D E$ 区域种植甲种花卉.根据设计要求，要满足点 $E$ 在 $A B$ 上， $A E = 2 B E$ ， $∠ D E C$ 是锐角，且 $t a n ∠ D E C = 2$ ，若种植水生植物每平方米需400元，种植甲种花卉每平方米需100元，求种植水生植物和种植甲种花卉所需总费用至少为多少元？

查看试题解析

四、第二十题

22. 设函数y₁= $\frac{k_{1}}{x}$ ，函数y₂=k₂x+b(k₁ ， k₂ ， b是常数，k₁≠0，k₂≠0)．

(1)、若函数y₁和函数y₂的图象交于点A(1，m)，点B(3，1)，
①求函数y₁ ， y₂的表达式：

②当2<x<3时，比较y₁与y₂的大小（直接写出结果）．

(2)、若点C(2，n)在函数y₁的图象上，点C先向下平移2个单位，再向左平移4个单位，得点D，点D恰好落在函数y₁的图象上，求n的值，

查看试题解析
23. 如图，在直角坐标系中，直线y=x+m与y= $\frac{m}{x}$ 在第一象限交于点A，且与x轴交于点C，AB⊥x轴，垂足为B，且S_△_AOB=1．

(1)、求m的值；

(2)、求△ABC的面积．

查看试题解析
24. 如图，在平面直角坐标系中，一次函数y=kx+b与反比例函数y= $\frac{m}{x}$ （m≠0）的图象交于点A（3，1），且过点B（0，﹣2）．

(1)、求反比例函数和一次函数的表达式；

(2)、如果点P是x轴上一点，且△ABP的面积是3，求点P的坐标．

查看试题解析
25. 如图，一次函数 $y = - \frac{1}{2} x + \frac{5}{2}$ 的图象与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象交于A，B两点，过点A做x轴的垂线，垂足为M， $△ A O M$ 面积为1.

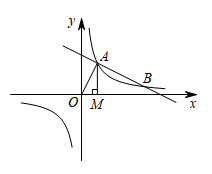(1)、求反比例函数的解析式；

(2)、在x轴上求一点P，使 $| P A - P B |$ 的值最大，并求出其最大值和P点坐标.

查看试题解析
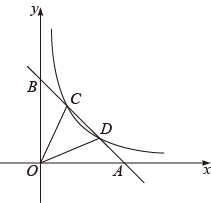26. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象与 $x$ 轴、 $y$ 轴分别交于 $A$ ， $B$ ，与反比例函数 $y = \frac{m}{x} (m > 0)$ 的图象交于点 $C (1 ， 2)$ ， $D (2 ， n)$ .

(1)、分别求出两个函数的表达式；

(2)、连接 $O C$ ， $O D$ ，求 $△ C O D$ 的面积.

查看试题解析
27. 在平面直角坐标系xOy中，直线y＝﹣ $\frac{1}{2}$ x+b与反比例函数y＝ $\frac{6}{x}$ 的图象交于A（2，m），B两点.

(1)、求直线AB的函数表达式；

(2)、如图1，过点A的直线分别与x轴，y轴交于点M，N，若AM=MN，连接BM，求△ABM的面积；

(3)、如图2，以AB为边作平行四边形ABCD，点C在y轴负半轴上，点D在反比例函数y＝ $\frac{k}{x}$ （k＜0）的图象上，线段AD与反比例函数y＝ $\frac{k}{x}$ （k＜0）的图象交于点E，若 $\frac{D E}{A E}$ ＝ $\frac{1}{2}$ ，求k的值.

查看试题解析
28. 如图，反比例函数 $y_{1} = \frac{k_{1}}{x} (x > 0)$ 与一次函数 $y_{2} = k_{2} x + n$ 相交于点A（1，4）和点B（4，1），直线 $y_{2}$ 的图象与y轴和x轴分别相交于点C和点D；

(1)、请直接写出当 $y_{1} \geq y_{2}$ 时自变量x的取值范围；

(2)、将一次函数 $y_{2} = k_{2} x + n$ 向下平移8个单位长度得到直线EF，直线EF与x和y轴分别交于点E和点F，抛物线 $y = a x^{2} + b x + c$ 过点A、D、E三点，求该抛物线的函数解析式（也称函数表达式）；

(3)、在（2）抛物线的对称轴上是否存在一点P，使得△PBF是以BF为斜边的直角三角形，若存在，请用尺规作图（圆规和无刻度直尺）画出点P所在位置，保留作图痕迹，并直接写出点P的坐标；若不存在，请说明理由．

查看试题解析