备考2023年中考数学杭州卷变式阶梯训练11-16题
试卷更新日期:2022-10-16 类型:二轮复习
一、第十一题
-
1. 计算: = ;(-2)2=2. 计算: .3. 计算: .4. 已知 ,若 ,则 .5. , 互为相反数, , 为自然数,则下列叙述正确的有个.
① , 互为相反数;② , 互为相反数;
③ , 互为相反数;④ , 互为相反数.
6. 任何实数a,可用[a]表示不大于a的最大整数,如[4]=4, ,现对72进行如下操作:72→ =8→ → =1,类似地:( 1 )对64只需进行次操作后变为1;
( 2 )只需进行3次操作后变为1的所有正整数中,最大的是.
7. 已知整数 的绝对值均小于5,且满 2021,则 的值为 .二、第十二题
-
8. 有5张仅有编号不同的卡片,编号分别是1,2,3,4,5.从中随机抽取一张,编号是偶数的概率等于9. 一个口袋中装有3个红球、2个绿球、1个黄球,每个球除颜色外其它都相同,搅匀后随机地从中摸出一个球是绿球的概率是 .10. 一箱饮品(每箱12瓶)中有2瓶的盖内印有“奖”字,小明的爸爸买了一箱这种品牌的饮品,但连续打开2瓶均未中奖,此时小明在剩下的饮品中任意拿一瓶,那么他拿出的这瓶饮品中奖的机会是 .11. 在物理实验课上,同学们用三个开关,两个灯泡、一个电源及若干条导线连接成如图所示的电路图,随机闭合图中的两个开关,有一个灯泡发光的概率是.
 12. 从-1,1,2中任取一个数作为k,从-1,0,1,2中任取一个数作为b,则一次函数的图象不经过第三象限的概率是.13. 有 6 张正面分别标有﹣1,﹣2,﹣3,0,1,4 的不透明卡片,它们除数字不同外,其余相同,现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为 m,则使关于 x 的分式方程 有正数解,且使一元二次方程 mx2+4x+4=0 有两个实数根的概率为.14. 在中, , , 是边上的中线,记且为正整数.则使关于的分式方程有正整数解的概率为 .
12. 从-1,1,2中任取一个数作为k,从-1,0,1,2中任取一个数作为b,则一次函数的图象不经过第三象限的概率是.13. 有 6 张正面分别标有﹣1,﹣2,﹣3,0,1,4 的不透明卡片,它们除数字不同外,其余相同,现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为 m,则使关于 x 的分式方程 有正数解,且使一元二次方程 mx2+4x+4=0 有两个实数根的概率为.14. 在中, , , 是边上的中线,记且为正整数.则使关于的分式方程有正整数解的概率为 .三、第十三题
-
15. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是16. 在平面直角坐标系中,一次函数y=kx和y=-x+3的图象如图所示,则二元一次方程组的解是 .
 17. 函数和的图象交于点 P (3,-2 ),则根据图象可得,关于 的二元一次方程组的解是 .18. 已知一次函数 和 ,假设 且 ,如果关于 、 的二元一次方程组 的解为 ,那么 0.19. 已知方程组 (a、b、c、k为常数, )的解为 ,则直线 和直线 的交点坐标为.20. 当m,n是正实数,且满足m+n=mn时,就称点P(m, )为“完美点”.已知点A(1,6)与点B的坐标满足y=﹣x+b,且点B是“完美点”.则点B的坐标是 .21. 平面直角坐标系中,直线与相交于点 , 下列结论中正确的是(填写序号).
17. 函数和的图象交于点 P (3,-2 ),则根据图象可得,关于 的二元一次方程组的解是 .18. 已知一次函数 和 ,假设 且 ,如果关于 、 的二元一次方程组 的解为 ,那么 0.19. 已知方程组 (a、b、c、k为常数, )的解为 ,则直线 和直线 的交点坐标为.20. 当m,n是正实数,且满足m+n=mn时,就称点P(m, )为“完美点”.已知点A(1,6)与点B的坐标满足y=﹣x+b,且点B是“完美点”.则点B的坐标是 .21. 平面直角坐标系中,直线与相交于点 , 下列结论中正确的是(填写序号).
①关于x,y的方程组的解是;
②关于x的不等式的解集是;
③ .
四、第十四题
-
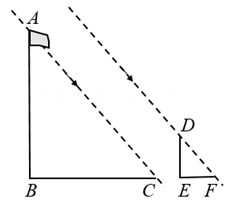
22. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.
 23. 在某一时刻,测得一根高为2m的竹竿的影长为3m,同时测得一根旗杆的影长为21m,那么这根旗杆的高度为m.24. 如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为米.
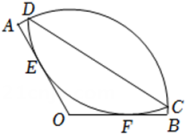
23. 在某一时刻,测得一根高为2m的竹竿的影长为3m,同时测得一根旗杆的影长为21m,那么这根旗杆的高度为m.24. 如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为米.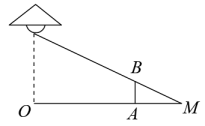 25. 《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为米.
25. 《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为米. 26. 如图所示,在平面直角坐标系xOy中,在直线x=1处放置反光镜Ⅰ,在y轴处放置一个需开缺口的挡板Ⅱ,缺口为线段AB,其中点A(0,1),点B在点A上方,在直线x=﹣2处放置一个挡板Ⅲ,从点O发出的光线经反光镜Ⅰ反射后,通过缺口AB照射在挡板Ⅲ上,若需在挡板Ⅲ形成长度为2的光线,则在挡板Ⅱ需开缺口AB的长度为.
26. 如图所示,在平面直角坐标系xOy中,在直线x=1处放置反光镜Ⅰ,在y轴处放置一个需开缺口的挡板Ⅱ,缺口为线段AB,其中点A(0,1),点B在点A上方,在直线x=﹣2处放置一个挡板Ⅲ,从点O发出的光线经反光镜Ⅰ反射后,通过缺口AB照射在挡板Ⅲ上,若需在挡板Ⅲ形成长度为2的光线,则在挡板Ⅱ需开缺口AB的长度为. 27. 图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 厘米,托架斜面长 厘米,它有C到F共4个档位调节角度,相邻两个档位间的距离为0.8厘米,档位C到B的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长 是15厘米,O是支点且 厘米(支架的厚度忽略不计).当支架调到E档时,点G离水平面的距离 为厘米;当支架从 档调到F档时,点D离水平面的距离下降了厘米.
27. 图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 厘米,托架斜面长 厘米,它有C到F共4个档位调节角度,相邻两个档位间的距离为0.8厘米,档位C到B的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长 是15厘米,O是支点且 厘米(支架的厚度忽略不计).当支架调到E档时,点G离水平面的距离 为厘米;当支架从 档调到F档时,点D离水平面的距离下降了厘米. 28. 如图1是某激光黑白A4纸张打印机的机身,其侧面示意图如图2, , .出纸盘 下方为一段以 为圆心的圆弧 ,与上部面板线段 相接于点 ,与 相切于点 .测得 , .进纸盘 可以随调节扣 向右平移, , .当 向右移动 至 时,点 , , 在同一直线上,则 的长度为 .若点 到 的距离为 , ,连结 ,线段 恰好过 的中点.若 ,则点 到直线 的距离为 .
28. 如图1是某激光黑白A4纸张打印机的机身,其侧面示意图如图2, , .出纸盘 下方为一段以 为圆心的圆弧 ,与上部面板线段 相接于点 ,与 相切于点 .测得 , .进纸盘 可以随调节扣 向右平移, , .当 向右移动 至 时,点 , , 在同一直线上,则 的长度为 .若点 到 的距离为 , ,连结 ,线段 恰好过 的中点.若 ,则点 到直线 的距离为 .
五、第十五题
-
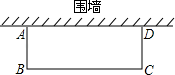
29. 某网络学习平台2019年的新注册用户数为100万,2021年的新注册用户数为169万,设新注册用户数的年平均增长率为x(x>0),则x= (用百分数表示).30. 某海洋养殖场每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖场第一年的可变成本为2.6万元,第三年的养殖成本为7.146万元,设可变成本平均每年增长的百分率为x,则可列方程为 .31. 如图,邻边不等的矩形花园ABCD,它的一边AD利用已有的围墙(墙足够长),另外三边所围的栅栏的总长度是18m,若矩形的面积为36m2 , 则AB的长度是m.
 32. 为积极响应国家的号召“房子是用来住的,不是用来炒的”,在宏观调控下,某楼盘商品房成交价由今年1月份的每平方米10000元下降到3月份的每平方米8100元,若今年前四个月房价每月的下降率保持一致,则小康爸爸在4月份用60万元在该楼盘买下一套80平方米的商品房.(请填入“能”或“不能”)33. 商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a , 最高销售限价b(b>a)以及常数k(0≤k≤1)确定实际销售价格为c=a+k(b﹣a),这里的k被称为乐观系数.经验表明,最佳乐观系数k恰好使得 ,据此可得,最佳乐观系数k的值等于 .34. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .
32. 为积极响应国家的号召“房子是用来住的,不是用来炒的”,在宏观调控下,某楼盘商品房成交价由今年1月份的每平方米10000元下降到3月份的每平方米8100元,若今年前四个月房价每月的下降率保持一致,则小康爸爸在4月份用60万元在该楼盘买下一套80平方米的商品房.(请填入“能”或“不能”)33. 商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a , 最高销售限价b(b>a)以及常数k(0≤k≤1)确定实际销售价格为c=a+k(b﹣a),这里的k被称为乐观系数.经验表明,最佳乐观系数k恰好使得 ,据此可得,最佳乐观系数k的值等于 .34. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 . 35. 如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为S1 , 空白部分的面积为S2 , 大正方形的边长为m,小正方形的边长为n,若 ,则 的值为.
35. 如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为S1 , 空白部分的面积为S2 , 大正方形的边长为m,小正方形的边长为n,若 ,则 的值为.
六、第十六题
-
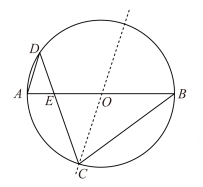
36. 如图是以点O为圆心,AB为直径的圆形纸片.点C在⊙O上,将该圆形纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E.若AD=ED,则∠B=度; 的值等于 .
 37. 如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CB,CD,BD,若 , 则的度数为是 .
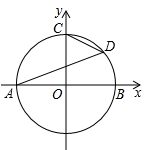
37. 如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CB,CD,BD,若 , 则的度数为是 . 38. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,且点A的坐标为(-2,0),D为第一象限内上的一点,若 , 则.
38. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,且点A的坐标为(-2,0),D为第一象限内上的一点,若 , 则.