2022-2023学年浙教版数学八(上)期中模拟测试(3)【考试范围:1-3章】
试卷更新日期:2022-10-16 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 在下面四个图标(图象)中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在△ABC中,AC=6,中线AD=10,则AB边的取值范围是( )A、16<AB<22 B、14<AB<26 C、16<AB<26 D、14<AB<223. 不等式 的最大整数解是( )A、0 B、 C、 D、4. 满足下列条件的三角形中,不是直角三角形的是( )A、三内角之比为3:4:5 B、三边长的平方之比为1:2:3 C、三边长之比为7:24:25 D、三内角之比为1:2:35. 如图所示 , 要说明≌ , 需添加的条件不能是( )
2. 在△ABC中,AC=6,中线AD=10,则AB边的取值范围是( )A、16<AB<22 B、14<AB<26 C、16<AB<26 D、14<AB<223. 不等式 的最大整数解是( )A、0 B、 C、 D、4. 满足下列条件的三角形中,不是直角三角形的是( )A、三内角之比为3:4:5 B、三边长的平方之比为1:2:3 C、三边长之比为7:24:25 D、三内角之比为1:2:35. 如图所示 , 要说明≌ , 需添加的条件不能是( ) A、 B、 C、 D、6. 如图,在△ABC中,AD平分∠BAC,点E在射线BC上,EF⊥AD于F,∠B=40°,∠ACE=72°,则∠E的度数为( )
A、 B、 C、 D、6. 如图,在△ABC中,AD平分∠BAC,点E在射线BC上,EF⊥AD于F,∠B=40°,∠ACE=72°,则∠E的度数为( ) A、68° B、56° C、34° D、32°7. 如图,已知平分 , 于 , , 则下列结论:;;;;其中正确结论的个数有( )
A、68° B、56° C、34° D、32°7. 如图,已知平分 , 于 , , 则下列结论:;;;;其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个8. 已知点P在 ABC的边BC上,且满足PA=PC , 则下列确定点P位置的尺规作图,正确的是( )A、
A、1个 B、2个 C、3个 D、4个8. 已知点P在 ABC的边BC上,且满足PA=PC , 则下列确定点P位置的尺规作图,正确的是( )A、 B、
B、 C、
C、 D、
D、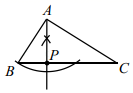 9. 如图,等边 中,D为AC中点,点P、Q分别为AB、AD上的点, , ,在BD上有一动点E,则 的最小值为( )
9. 如图,等边 中,D为AC中点,点P、Q分别为AB、AD上的点, , ,在BD上有一动点E,则 的最小值为( )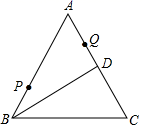 A、7 B、8 C、10 D、1210. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( )
A、7 B、8 C、10 D、1210. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( ) A、26 B、35 C、47 D、94
A、26 B、35 C、47 D、94二、填空题(每题4分,共24分)
-
11. 命题“若a2>b2则a>b”是命题(填“真”或“假”),它的逆命题是 .12. 不等式 的最小负整数解.13. 如图,在中, , 的顶点在的边上,点在的延长线上, , 且 , 若 , 则的度数为 .
 14. 如图,直线AD为 ABC的对称轴,BC=6,AD=4,则图中阴影部分的面积为 .
14. 如图,直线AD为 ABC的对称轴,BC=6,AD=4,则图中阴影部分的面积为 .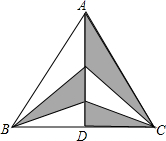 15. 如图,在△ABC中,点D在边BC上,AB=AD,点E,点F分别是AC,BD的中点,EF=3,则AC的长为.
15. 如图,在△ABC中,点D在边BC上,AB=AD,点E,点F分别是AC,BD的中点,EF=3,则AC的长为. 16. 如图,在△ABC中,∠ACB=90°,以AC,BC和AB为边向上作正方形ACED和正方形BCMI和正方形ABGF,点G落在MI上,若AC+BC=7,空白部分面积为16,则图中阴影部分的面积是 .
16. 如图,在△ABC中,∠ACB=90°,以AC,BC和AB为边向上作正方形ACED和正方形BCMI和正方形ABGF,点G落在MI上,若AC+BC=7,空白部分面积为16,则图中阴影部分的面积是 .
三、解答题(共8题,共66分)
-
17. 在图①补充2个小方块,在图②、③、④中分别补充3个小方块,分别使它们成为轴对称图形.
 18. 如图,O是线段AC、DB的交点,且AC=BD,AB=DC,
18. 如图,O是线段AC、DB的交点,且AC=BD,AB=DC,求证:OB=OC.
 19.(1)、解方程组;(2)、解不等式组: , 并把它的解集在数轴上表示出来.
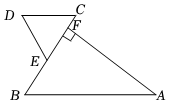
19.(1)、解方程组;(2)、解不等式组: , 并把它的解集在数轴上表示出来. 20. 如图,在 中, , ,F为 延长线上一点,点E在 上,且 .
20. 如图,在 中, , ,F为 延长线上一点,点E在 上,且 .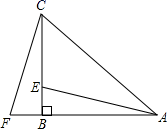 (1)、求证: ;(2)、若 ,求 的度数.21. 有大小两种货车,2辆大货车与3辆小货车一次可以运货 , 5辆大货车与6辆小货车一次可以运货 .(1)、每辆大货车与每辆小货车一次分别可以运货多少吨?(2)、若每辆大货车的租金为400元,每辆小货车的租金为300元,某公司计划租用这两种货车共20辆把货物一次性运走,要使总费用不超过7000元,一共有多少种租车方案?22. 如图①,△ABC 和△CDE是等边三角形,连接AE、BD , 连接DA并延长交BC于F , AE=CE .
(1)、求证: ;(2)、若 ,求 的度数.21. 有大小两种货车,2辆大货车与3辆小货车一次可以运货 , 5辆大货车与6辆小货车一次可以运货 .(1)、每辆大货车与每辆小货车一次分别可以运货多少吨?(2)、若每辆大货车的租金为400元,每辆小货车的租金为300元,某公司计划租用这两种货车共20辆把货物一次性运走,要使总费用不超过7000元,一共有多少种租车方案?22. 如图①,△ABC 和△CDE是等边三角形,连接AE、BD , 连接DA并延长交BC于F , AE=CE . (1)、求证: ;(2)、如图②,作 的边 上的高线 ,交 的延长线于点P,求证: .23. 如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题:
(1)、求证: ;(2)、如图②,作 的边 上的高线 ,交 的延长线于点P,求证: .23. 如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题: (1)、如果AB=AC,∠BAC=90°.
(1)、如果AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为,数量关系为.(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)、如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?画出相应的图形,并说明理由.
24. 我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式,这种方法称之为“无字证明”,它比严谨的数学证明更为优雅与有条理.三国时代东吴数学家赵爽(字君卿,约公元3世纪)在《勾股圆方图注》一书中用割补的方法构造了“无字证明”图形(如图①).其中四个直角三角形较长的直角边长都为a , 较短的直角边长都为b , 斜边长都为c , 大正方形的面积可以表示为c2 , 也可以表示为4× ab+(a﹣b)2 , 由此推导出一个重要的定理. (1)、此图可以推导出你学过的什么定理?请写出定理的内容;(2)、图②为美国第二十任总统伽菲尔德创造的“无字证明”图形,请你利用图②推导(1)中的定理.(3)、根据(1)中的定理,解决下面的问题:如图③,在一条东西走向河流的一侧有一村庄C , 河边原有两个取水点A , B , 其中AB=AC , 由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH , 且CH⊥AB . 测得CH=1.2千米,HB=0.9千米,求新路CH比原路CA少多少千米?
(1)、此图可以推导出你学过的什么定理?请写出定理的内容;(2)、图②为美国第二十任总统伽菲尔德创造的“无字证明”图形,请你利用图②推导(1)中的定理.(3)、根据(1)中的定理,解决下面的问题:如图③,在一条东西走向河流的一侧有一村庄C , 河边原有两个取水点A , B , 其中AB=AC , 由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH , 且CH⊥AB . 测得CH=1.2千米,HB=0.9千米,求新路CH比原路CA少多少千米?