2022-2023学年浙教版数学八（上）期中模拟测试（2）【考试范围：1.1-3.2】
试卷更新日期：2022-10-16 类型：期中考试
一、单选题（每题3分，共30分）
-
1. 在一些美术字中，有的汉字是轴对称图形.下面4个汉字中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
2. 四根长度分别为、、、的木条，以其中三根的长为边长，制作成一个三角形框架，那么这个框架的周长可能是（ ）A、 B、 C、 D、3. 如图用直尺和圆规作已知角的平分线的示意图，由≌可得 ， 由作图的过程可知，说明≌的依据是（ ）
A、 B、 C、 D、4. 如图，线段AB，BC的垂直平分线 ， 相交于点O.若 ， 则（ ）
A、50° B、80° C、90° D、100°5. 下列选项中，可以用来说明命题“两个锐角的和是锐角”是假命题的反例是（ ）A、两个角分别为13°，45° B、两个角分别为40°，45° C、两个角分别为45°，45° D、两个角分别为105°，45°6. 下列尺规作图分别表示：①作一个角的平分线，②作一个角等于已知角．③作一条线段的垂直平分线．其中作法正确的是（ ）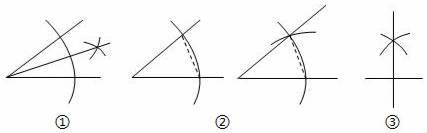
A、①②③ B、②③ C、①③ D、①②7. 已知 的周长是16，且 ，又 ，D为垂足，若 的周长是12，则AD的长为（ ）A、7 B、6 C、5 D、48. 下面图形能够验证勾股定理的有（ ）个
A、4个 B、3个 C、2个 D、1个9. 如图，M，A，N是直线l上的三点， ， ， P是直线l外一点，且 ， ， 若动点Q从点M出发，向点N移动，移动到点N停止，在APQ形状的变化过程中，依次出现的特殊三角形是（ ）
A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形10. 如图，△ABC与△BDE是全等的等边三角形，且A、B、D三点共线，AE、CD交于点O，∠AEB＝∠EAB．现有如下结论：①∠AED＝90°；②∠BCD+∠AEB＝60°，③OB⊥AD；④AE＝CD；⑤OB平分∠CBE，平分∠AOD；⑥AO+OB＝AD；一定成立的有（ ）个．
A、5个 B、6个 C、3个 D、4个二、填空题（每题4分，共24分）
-
11. 用不等式表示“x的4倍小于3”为.12. 三角形的两边长分别为4和6，那么第三边的取值范围是 ．13. 如图，D、E分别是△ABC边AB，BC上的点，AD＝2BD，BE＝CE，设△ADF的面积为S1 ， △FCE的面积为S2 ， 若S△ABC＝24，则S1﹣S2的值为 ．
14. 若直角三角形斜边上的高和中线长分别是 ， ，则它的面积是 .15. 如图，在 中， ， ，高 .作点H关于 ， 的对称点D，E，连接 交 于点P，交 于点Q；连接 ， ， ， .下列结论：① ；② ；③五边形 的面积是24；④ 的周长为6.其中正确结论是.（填写序号）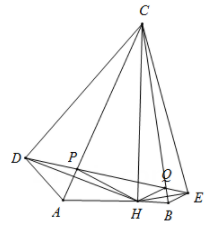
16. 若 ，则 （填“＞”或“＝”或“＜”）.三、解答题（共8题，共66分）
-
17. 如图，已知△ABC.
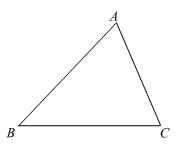
⑴尺规作图：求作∠BAC的角平分线AD，交BC于点D.（保留作图痕迹，不写作法）
⑵若DE⊥AB，DF⊥AC，垂足分别为E，F，连结EF.请依据上述几何语言，画出完整图形，再判断AD是否垂直平分EF，并说明理由.
18. 如图某海滨浴场的岸边4C可近似地看成直线，位于岸边A处的救生员发现海中B处有人求救，救生员没有从A处游向B处，而是沿岸边自A处跑到距离B处最近的C处，然后从C处游向B处．已知∠BAC=45°，AC=300米，救生员在岸边行进速度为6米/秒，在海中行进的速度为2米/秒．请分析救生员的路线选择是否正确．
19. 已知：如图点A、B、C在同一直线上，且AM＝AN，BM＝BN，求证：CM＝CN．
20. 已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．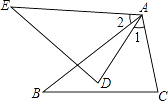
21. 如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE于B，DE⊥BE于E，且AB＝DE，BF＝CE.求证：
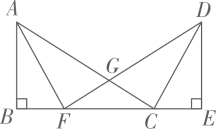(1)、GF＝GC；(2)、△AFG≌△DCG.22. 如图，≌ ， AC和AE，AB和AD是对应边，点E在边BC上，AB与DE交于点F．
(1)、求证：；(2)、若 ， 求的度数．
