2022-2023学年浙教版数学八(上)期中模拟测试(1)【考试范围:1-2章】
试卷更新日期:2022-10-16 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 下列各组线段能构成三角形的是( )A、2cm,2cm,4cm B、2cm,3cm,4cm C、2cm,2cm,5cm D、2cm,3cm,6cm2. 如图图案中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,在△ABC中,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A的度数为( )
3. 如图,在△ABC中,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A的度数为( ) A、30° B、45° C、20° D、22.5°4. △ABC≌△DEF,且△ABC的周长为100cm,A、B分别与D、E对应,且AB=35cm,DF=30cm,则EF的长为( )A、35cm B、30cm C、45cm D、55cm5. △ABC的三边为a,b,c且(a+b)(a﹣b)=c2 , 则该三角形是( )A、锐角三角形 B、以c为斜边的直角三角形 C、以b为斜边的直角三角形 D、以a为斜边的直角三角形6. 如图,是的中线,交的延长于点 , , , 则的取值可能是( )
A、30° B、45° C、20° D、22.5°4. △ABC≌△DEF,且△ABC的周长为100cm,A、B分别与D、E对应,且AB=35cm,DF=30cm,则EF的长为( )A、35cm B、30cm C、45cm D、55cm5. △ABC的三边为a,b,c且(a+b)(a﹣b)=c2 , 则该三角形是( )A、锐角三角形 B、以c为斜边的直角三角形 C、以b为斜边的直角三角形 D、以a为斜边的直角三角形6. 如图,是的中线,交的延长于点 , , , 则的取值可能是( ) A、3 B、6 C、8 D、127. 已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A、3 B、6 C、8 D、127. 已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( ) A、 B、 C、 D、8. 如图所示,、、分别表示的三边长,则下面与一定全等的三角形是( )
A、 B、 C、 D、8. 如图所示,、、分别表示的三边长,则下面与一定全等的三角形是( )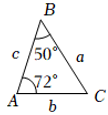 A、
A、 B、
B、 C、
C、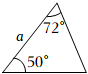 D、
D、 9. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,BE⊥AC,CF⊥AB,垂足分别为E,F.则下列四个结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到边AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF;⑤BC=AD.其中,正确的个数为( )
9. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,BE⊥AC,CF⊥AB,垂足分别为E,F.则下列四个结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到边AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF;⑤BC=AD.其中,正确的个数为( ) A、2个 B、3个 C、4个 D、5个10. 如图,网格线的交点称为格点,任取 个格点构成等腰三角形,则下列可以作为腰长的是( )
A、2个 B、3个 C、4个 D、5个10. 如图,网格线的交点称为格点,任取 个格点构成等腰三角形,则下列可以作为腰长的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 命题“等腰三角形两腰上的高相等”的逆命题是 , 这个逆命题是命题.12. 如图,在△ABC中,AD⊥BC于点D , BD=DC , 若BC=6,AD=7,则图中阴影部分图形的面积为 .
 13. 一个三角形的三条高线的交点在三角形的外部,则这个三角形是 三角形14. 如图,已知 中, 平分 ,且 ,则点D到 边的距离为.
13. 一个三角形的三条高线的交点在三角形的外部,则这个三角形是 三角形14. 如图,已知 中, 平分 ,且 ,则点D到 边的距离为. 15. 如图,每个小正方形的边长都为1,△ABC是格点三角形,点D为AC的中点,则线段BD的长为 .
15. 如图,每个小正方形的边长都为1,△ABC是格点三角形,点D为AC的中点,则线段BD的长为 .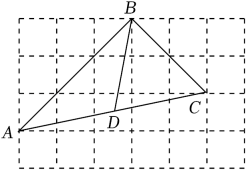 16. 若a,b为等腰 的两边,且满足 ,则 的周长为.
16. 若a,b为等腰 的两边,且满足 ,则 的周长为.三、解答题(共7题,共66分)
-
17. 作图题:要求保留作图痕迹,不写作法
 (1)、作线段AC的垂直平分线,分别交AC、BC于E、F.在直线EF上找一点P,使得点P到射线AB,AC的距离相等.(2)、若AB=6,BC=8,连接AF,求△ABF的周长.18. 如图,在△ABC中, , D、E是△ABC内的两点,AD平分∠BAC, . 若 , , 求BC的长.
(1)、作线段AC的垂直平分线,分别交AC、BC于E、F.在直线EF上找一点P,使得点P到射线AB,AC的距离相等.(2)、若AB=6,BC=8,连接AF,求△ABF的周长.18. 如图,在△ABC中, , D、E是△ABC内的两点,AD平分∠BAC, . 若 , , 求BC的长.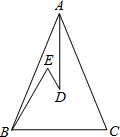 19. 如图, 中, , 平分 .若 交 于F , 求证: .
19. 如图, 中, , 平分 .若 交 于F , 求证: .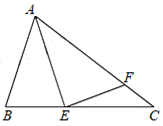 20.如图, △ABC中, AB=AC ,D、E分别是AB、AC上的点,且 ∠ABE=∠ACD ,BE、CD交于点O,求证: △OBC是等腰三角形.
20.如图, △ABC中, AB=AC ,D、E分别是AB、AC上的点,且 ∠ABE=∠ACD ,BE、CD交于点O,求证: △OBC是等腰三角形.
 21. 已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
21. 已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.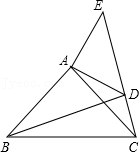 (1)、求证:△BAD≌△CAE;(2)、试猜想BD、CE有何特殊位置关系,并证明.22. 2021年10月10日是辛亥革命110周年纪念日.为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神,社区开展了系列纪念活动.如图,有一块四边形空地,社区计划将其布置成展区,陈列有关辛亥革命的历史图片.现测得 , , ,且 .
(1)、求证:△BAD≌△CAE;(2)、试猜想BD、CE有何特殊位置关系,并证明.22. 2021年10月10日是辛亥革命110周年纪念日.为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神,社区开展了系列纪念活动.如图,有一块四边形空地,社区计划将其布置成展区,陈列有关辛亥革命的历史图片.现测得 , , ,且 . (1)、试说明 ;(2)、求四边形展区(阴影部分)的面积.23. 如图1,在等边△ABC中,线段AM为BC边上的高线.动点D在线段AM(点D与点A重合除外)上时,以CD为一边且在CD的下方作等边△CDE,连结BE.
(1)、试说明 ;(2)、求四边形展区(阴影部分)的面积.23. 如图1,在等边△ABC中,线段AM为BC边上的高线.动点D在线段AM(点D与点A重合除外)上时,以CD为一边且在CD的下方作等边△CDE,连结BE. (1)、若DM=MC,则∠ACD=度,∠BCE=度;(2)、判断AD与BE是否相等,请说明理由;(3)、如图2,若AB=12,P、Q两点在直线BE上且满足CP=CQ=10,试求PQ的长.(4)、在第(3)小题的条件下,当点D在线段AM的延长线(或反向延长线)上时,判断PQ的长是否为定值,若是,请直接写出PQ的长;若不是,请简单说明理由.
(1)、若DM=MC,则∠ACD=度,∠BCE=度;(2)、判断AD与BE是否相等,请说明理由;(3)、如图2,若AB=12,P、Q两点在直线BE上且满足CP=CQ=10,试求PQ的长.(4)、在第(3)小题的条件下,当点D在线段AM的延长线(或反向延长线)上时,判断PQ的长是否为定值,若是,请直接写出PQ的长;若不是,请简单说明理由.