2022-2023学年浙教版数学七(上)期中模拟测试(1)
试卷更新日期:2022-10-15 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 规定向东为正,向西为负.那么小明走﹣30米表示( )A、小明向东走30米 B、小明向西走30米 C、小明向南走30米 D、小明向北走30米2. 两个有理数的和为0,则这两个数( )A、都是0 B、至少有一个为0 C、互为相反数 D、一正一负3. 下列各数: , , , , , 其中无理数有( )A、4个 B、3个 C、2个 D、1个4. 下列式子中,书写正确的是( )A、 B、 C、 D、 米5. 下列结论正确的是 ( )A、-2的倒数是2 B、64的平方根是8 C、16的立方根为4 D、算术平方根是本身的数为0和16. 下列计算,结果正确的是( )A、4a2b﹣5ab2=﹣a2﹣b B、5a2+3a2=8a4 C、2x+3y=5xy D、3xy﹣5yx=﹣2xy7. 下列说法中,正确的是( )A、多项式 是二次三项式 B、单项式 的系数是 C、单项式 和 是同类项 D、 是单项式8. 下列说法中,不正确的个数有( ).
①所有的正数都是整数. ② 一定是正数. ③无限小数一定是无理数.
④ 没有平方根. ⑤不是正数的数一定是负数. ⑥带根号的一定是无理数.
A、3个 B、4个 C、5个 D、6个9. 已知点A,B,C,D在数轴上的位置如图所示,且相邻两点之间的距离均为1个单位长度.若点A,B,C,D分别表示数 , b,c,d,且满足 , 则b的值为( )
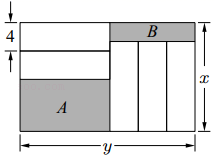
 A、 B、 C、 D、10. 如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为4cm,下列说法中正确的有( )
A、 B、 C、 D、10. 如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为4cm,下列说法中正确的有( )①小长方形的较长边为y﹣12;
②阴影A的较短边和阴影B的较短边之和为x﹣y+4;
③若x为定值,则阴影A和阴影B的周长和为定值;
④当x=20时,阴影A和阴影B的面积和为定值.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题4分,共24分)
-
11. 习总书记提出要“厉行节约,杜绝舌尖上的浪费”.假如我国每人每餐少浪费一粒米,一年就能节省约32400000斤粮食.32400000用科学记数法表示为 .12. 比较大小:(1)、--(2)、-0.213. 香蕉的单价为a元/千克,苹果的单价为b元/千克,买2千克苹果和3千克香蕉共需元.14. 有理数 、 在数轴上的位置如图所示,下列说法:① ,② ,③ ,④ ,⑤ ;其中正确的序号有.
 15. 如果代数﹣2y2+y﹣1的值为10,那么代数式4y2﹣2y+5的值为 .16. 若是不为2的有理数,我们把称为的“哈利数”,如3的“哈利数”是 , 的“哈利数”是 , 已知 , 是的“哈利数”,是的“哈利数”,是的“哈利数”,…,依此类推,则等于.
15. 如果代数﹣2y2+y﹣1的值为10,那么代数式4y2﹣2y+5的值为 .16. 若是不为2的有理数,我们把称为的“哈利数”,如3的“哈利数”是 , 的“哈利数”是 , 已知 , 是的“哈利数”,是的“哈利数”,是的“哈利数”,…,依此类推,则等于.三、解答题(共7题,共66分)
-
17. 计算:(1)、(2)、18. 如果│a+1│+│2b-3│+│c-1│=0,那么 值是多少?19. 求代数式的值.(1)、(6a2﹣2ab)﹣2(3a2+4ab﹣b2)其中a= , b=﹣1.(2)、已知A=a2﹣2ab+b2 , B=a2+2ab+b2
①求2A﹣B;
②如果2A﹣3B+C=0,那么C的表达式是什么?
20. 阅读下面计算2(﹣4a+3b)﹣5(a﹣2b)的解题过程.解:原式=(﹣8a+6b)﹣(5a﹣10b)(第1步)
=﹣8a+6b﹣5a﹣10b(第2步)
=﹣13a+16b.(第3步)
请回答:
(1)、上面解题过程中从第步起开始出错了.(2)、请给出正确的计算过程.21. 如图1,依次连接2×2方格四条边的中点,得到一个阴影正方形,设每一方格的边长为1个单位,则这个阴影正方形的边长为.
 (1)、图1中阴影正方形的边长为 ;点P表示的实数为;(2)、如图2,在4×4方格中阴影正方形的边长为a.
(1)、图1中阴影正方形的边长为 ;点P表示的实数为;(2)、如图2,在4×4方格中阴影正方形的边长为a.①写出边长a的值.
②请仿照(1)中的作图在数轴上表示实数﹣a+1.
22. 如图,某公园计划修建一块长方形花坛,宽为 , 长为 , 在花坛两端及中间铺设半圆型花圃, 其他区域铺设草坪,设铺设草坪区域的面积为. (1)、用含a,b的代数式表示.(2)、当米, 米时,求的值(结果保留).23. (阅读理解):A,B,C为数轴上三点,若点C到A的距离CA是点C到B的距离CB的2倍,就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离CA是2,到点B的距离CB是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离DA是1,到点B的距离DB是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
(1)、用含a,b的代数式表示.(2)、当米, 米时,求的值(结果保留).23. (阅读理解):A,B,C为数轴上三点,若点C到A的距离CA是点C到B的距离CB的2倍,就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离CA是2,到点B的距离CB是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离DA是1,到点B的距离DB是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.(知识运用):
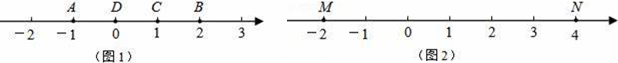
 (1)、如图1,表示数和的点是(A,B)的好点;(2)、如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.
(1)、如图1,表示数和的点是(A,B)的好点;(2)、如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.①表示数的点是(M,N)的好点;
②表示数的点是(N,M)的好点;
(3)、如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动.当t为何值时,P、A和B中恰有一个点为其余两点的好点?