2022-2023学年浙教版数学九上期中复习专题8 相似三角形

试卷更新日期：2022-10-15 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知 $\frac{x}{y} = \frac{3}{5}$ ，则 $\frac{x}{x + y}$ 的值为（）

A、 $\frac{2}{5}$ B、 $\frac{3}{8}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
2. 如图，l₁∥l₂∥l₃ ，直线a，b与l₁ ， l₂ ， l₃分别交于点A，B，C和点D，E，F．若 $\frac{A B}{B C} = \frac{2}{3}$ ， DE＝4，则DF的长是（）

A、 $\frac{8}{3}$ B、 $\frac{20}{3}$ C、6 D、10

查看试题解析
3. 如图，已知△ABC∽△DEF，若∠A＝35°，∠B＝65°，则∠F的度数是（）

A、30° B、35° C、80° D、100°

查看试题解析
4. 已知图中有两组三角形，其边长和角的度数已在图上标注，对于各组中的两个三角形而言，下列说法正确的是（）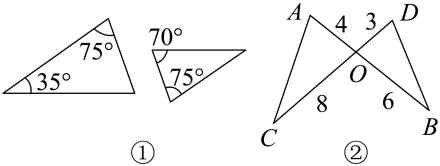

A、都相似 B、都不相似 C、只有①相似 D、只有②相似

查看试题解析
5. 下列各组中的四条线段成比例的是（）

A、1cm，2cm，3cm，4cm B、2cm，3cm，4cm，5cm C、2cm，3cm，4cm，6cm D、3cm，4cm，6cm，9cm

查看试题解析
6. 如图，如果 $∠ B A D = ∠ C A E$ ，那么添加下列一个条件后，仍不能确定 $△ A B C$ ∽ $△ A D E$ 的是（）

A、 $∠ B = ∠ D$ B、 $\frac{A B}{A D} = \frac{D E}{B C}$ C、 $∠ C = ∠ A E D$ D、 $\frac{A B}{A D} = \frac{A C}{A E}$

查看试题解析
7. 如图，在一张台球桌上，一球在点A处，要从A处击打出去，经球台边挡板CD反射击中B球．作AC⊥CD于点C，BD⊥CD于点D．已知∠AEC＝∠BED，AC＝10cm，BD＝15cm，CD＝20cm，若球手恰好能击中B球，则DE的长为（）

A、8cm B、10cm C、12cm D、 $\frac{40}{3}$ cm

查看试题解析
8. 如图，在△ABC中，点D是AB边上的一点，若∠ACD=∠B，AD＝1，AC＝2，△ADC的面积为1，则△BCD的面积为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 如图， $B D$ 是 $△ A B C$ 的角平分线， $D E ∥ B C$ 交 $A B$ 于点E，若 $△ A B C$ 的重心G在 $D E$ 上，则 $A B ： B C$ 的值是（）

A、 $3 ： 2$ B、 $7 ： 4$ C、 $2 ： 1$ D、 $8 ： 5$

查看试题解析
10. 如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（）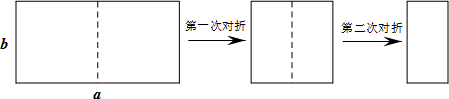

A、a＝ $\sqrt{2}$ b B、a＝2b C、a＝2 $\sqrt{2}$ b D、a＝4b

查看试题解析

二、填空题（每题4分，共24分）

11. 相邻两边长的比值是黄金分割数的矩形，叫作黄金矩形．从外形看，它最具美感．现在想要制作一张“黄金矩形”的贺年卡，如果较长的一条边长等于26厘米，那么相邻一条边的边长等于厘米．

查看试题解析
12. 如图，在 $△ A B C$ 中， $A B = 6$ ， $A C = 4$ ， D是 $A B$ 的中点，过D点的直线交 $A C$ 于点Q，若使 $△ A D Q$ 与 $△ A B C$ 相似，则 $A Q$ 的长度为．

查看试题解析
13. 如图，在△ABC中，∠ACB＝90°，CD⊥AB，DE⊥BC，垂足分别为点D，E，则图中与△ABC相似的三角形个数有个.

查看试题解析
14. 如图1，一张矩形纸片 $A B C D$ ，点 $E$ 、 $F$ 分别在 $A B$ ， $C D$ 上，点 $G$ ， $H$ 分别在 $A F$ 、 $E C$ 上，现将该纸片沿 $A F$ ， $G H$ ， $E C$ 剪开，拼成如图2所示的矩形，已知 $D F$ ： $A D = 5$ ： $12$ ， $G H = 6$ ，则 $A D$ 的长是．

查看试题解析
15. 如图，已知M、N为 $△ A B C$ 的边 $B C$ 上的两点，且满足 $B M = M N = N C$ ，一条平行于 $A C$ 的直线分别交 $A B$ 、 $A M$ 、 $A N$ 的延长线于点D、E、F，则 $\frac{E F}{D E} =$ ．

查看试题解析
16. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．将小正方形对角线EF双向延长，分别交边AB，和边BC的延长线于点G，H．若大正方形与小正方形的面积之比为5，GH＝2 $\sqrt{5}$ ，则大正方形的边长为．

查看试题解析

三、解答题（共8题，共66分）

17. 已知实数x、y、z满足 $\frac{x}{3} = \frac{y}{5} = \frac{z}{2}$ ，且x﹣2y+3z＝﹣2．求： $\frac{x + y}{2 y - 3 z}$ 的值．

查看试题解析
18. 如图，在△ABC中，AB＝10cm，BC＝20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果点P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．

查看试题解析
19. 如图，△ABC的三个顶点都在方格纸的格点上，请按要求在方格纸内作图．

(1)、在图甲中以点A为位似中心，作△ABC的位似图形，使得与△ABC的位似比为1：2．

(2)、在图乙中作出△ABC的相似三角形，使得该三角形的顶点都在格点上，且与△ABC相似比为1： $\sqrt{2}$ ．

查看试题解析
20.

(1)、已知a＝4.5，b＝2，c是a，b的比例中项，求c；

(2)、如图，C是AB的黄金分割点，且AC＞BC，AB＝4，求AC的长．

查看试题解析
21. 如图，△ABC中，DE∥BC，EF∥AB

求证：△ADE∽△EFC.

查看试题解析
22. 如图，△ABC中，∠C＝90°，AC＝4cm，BC＝3cm，动点P从点B出发以1cm/s速度向点C移动，同时动点Q从C出发以2cm/s的速度向点A移动，其中一个点到终点另一个点也随之停止.设它们的运动时间为t.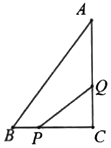

(1)、根据题意知：CQ＝， CP＝；（用含t的代数式表示）；

(2)、运动几秒时，△CPQ与△CBA相似？

查看试题解析
23. 阅读下列材料，完成任务
小明同学酷爱数学，勤于探索研究，他画了一个三角形ABC，并画出其中一个外角 $∠ C A E$ 的角平分线，与BC的延长线交于点N，小明通过测量发现，该图形中的线段有特殊的关系： $\frac{A B}{A C} = \frac{N B}{N C}$ ，他想证明自己的发现．下面是部分证明过程：

证明：过点C作 $C D ∥ A N$ 交AB于点D，则 $\frac{A B}{A D} = \frac{N B}{N C}$ （第一步），

∴ $∠ A C D = ∠ C A N$ ， $∠ A D C = ∠ E A N$ （第二步）

…

请回答下面问题：

(1)、小明部分证明过程中，第一步的依据是；

(2)、请完成证明的剩余部分；

(3)、若 $A B = 6 \sqrt{3}$ ， $A C = 6$ ， $∠ B A C = 30 °$ ，请求出CN的长．

查看试题解析
24. 【问题提出】已知有两个Rt△ABC和Rt△A'B′C'，其中∠C＝∠C′＝90°，∠A＝60°，∠A′＝45°．

(1)、如图1，作线段CD，C′D′，分别交AB于点D，交A'B′于点D′，使得∠BCD＝45°，∠B'C′D'＝30°，问△BCD与△B'C′D'，△ACD与△A′C′D′是否相似？并选择其中相似的一对三角形，说明理由．

(2)、如图2，作线段AD，B'D′，分别交BC于点D，交A'C'于点D，若△ACD与△B′C′D′、△ABD与△A′B'D'均相似，求∠CAD，∠C'B'D′的度数．

(3)、【拓展思考】已知任意两个不相似的直角三角形，能否分别作一条直线对其进行分割，使其中一个三角形所分割得到的两个三角形与另一个三角形所分割得到的两个三角形分别对应相似？如果可以，请直接画出一种分割示意图；如果不能，请说明理由．

查看试题解析
25. 四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的“相似对角线”.

(1)、如图1，在四边形ABCD中，∠ABC＝100°，∠ADC＝130°，BD≠BC，对角线BD平分∠ABC.求证：BD是四边形ABCD的“相似对角线”；

(2)、如图2，已知格点△ABC，请你在正方形网格中画出所有的格点四边形ABCD，使四边形ABCD是以AC为“相似对角线”的四边形；（注：顶点在小正方形顶点处的多边形称为格点多边形）

(3)、如图3，四边形AOBC中，点A在射线OP： $y = \sqrt{3} x$ （x≥0）上，点B在x轴正半轴上，对角线OC平分∠AOB，连接AB.若OC是四边形AOBC的“相似对角线”，S_△AOB＝6 $\sqrt{3}$ ，求点C的坐标.

查看试题解析