2022-2023学年浙教版数学九上期中复习专题6 图形的旋转
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列事件中,属于旋转运动的是( )A、小明向北走了4米 B、小明在荡秋千 C、电梯从1楼到12楼 D、一物体从高空坠下2. 小明将图
 案绕某点连续旋转若干次,每次旋转相同角度 , 设计出一个外轮廓为正六边形的图案(如图),则可以为( )
案绕某点连续旋转若干次,每次旋转相同角度 , 设计出一个外轮廓为正六边形的图案(如图),则可以为( ) A、30° B、60° C、90° D、120°3. 如图,该图形围绕其中心点O按下列角度旋转后,能与其自身重合的是( )
A、30° B、60° C、90° D、120°3. 如图,该图形围绕其中心点O按下列角度旋转后,能与其自身重合的是( ) A、 B、 C、 D、4. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( )
A、 B、 C、 D、4. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( ) A、(a,a) B、 C、 D、5. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为144.AE=13.则DE的长为( )
A、(a,a) B、 C、 D、5. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为144.AE=13.则DE的长为( )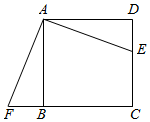 A、2 B、 C、4 D、56. 如图,在平面直角坐标系中,O为坐标原点,为 , 点A的坐标是 , , 把绕点A按顺时针方向旋转后,得到 , 则的外接圆圆心坐标是( )
A、2 B、 C、4 D、56. 如图,在平面直角坐标系中,O为坐标原点,为 , 点A的坐标是 , , 把绕点A按顺时针方向旋转后,得到 , 则的外接圆圆心坐标是( ) A、 B、 C、 D、7.
A、 B、 C、 D、7.如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
 A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转120°后形成的 D、以轴心为旋转中心,旋转120°、240°后形成的8. 如图,正方形ABCD的边长为1,将其绕顶点C旋转,得到正方形CEFG,在旋转过程中,则线段AE的最小值为( )
A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转120°后形成的 D、以轴心为旋转中心,旋转120°、240°后形成的8. 如图,正方形ABCD的边长为1,将其绕顶点C旋转,得到正方形CEFG,在旋转过程中,则线段AE的最小值为( ) A、 B、 -1 C、0.5 D、9. 如图,△ABC中,∠ACB=90°,∠ABC=40°,将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在边AB上,则∠CAA'的度数是( )
A、 B、 -1 C、0.5 D、9. 如图,△ABC中,∠ACB=90°,∠ABC=40°,将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在边AB上,则∠CAA'的度数是( )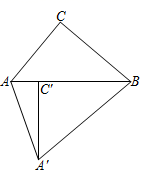 A、50° B、70° C、110° D、120°10. 如图,将 ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在AC边上时,连结AD,若∠DAC=75°,AC=2BC=2,则图中阴影部分的面积为( )
A、50° B、70° C、110° D、120°10. 如图,将 ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在AC边上时,连结AD,若∠DAC=75°,AC=2BC=2,则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. △ABC绕着A点旋转后得到△A'B'C',若∠BAC'=130°,∠BAC=80°,则旋转角等于 .12. 一个等边三角形绕其旋转中心至少旋转度,才能与自身重合.13. 把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6厘米,DC=7厘米.把三角板DCE绕点C顺时针旋转15°得到 , 如图(2),这时AB与相交于点O,与相交于点F.则=cm.
 14. 如图,将绕点按顺时针旋转一定角度得到 , 点的对应点恰好落在边上,若 , , 则的长为 .
14. 如图,将绕点按顺时针旋转一定角度得到 , 点的对应点恰好落在边上,若 , , 则的长为 . 15. 点A(﹣2,﹣1)绕点B(﹣1,0)旋转180°得到点C.则点C坐标为 .16. 已知在△ABC中,∠C=90°,AC=12,BC=5,在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′落直线AB上,那么AA′的长为 .
15. 点A(﹣2,﹣1)绕点B(﹣1,0)旋转180°得到点C.则点C坐标为 .16. 已知在△ABC中,∠C=90°,AC=12,BC=5,在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′落直线AB上,那么AA′的长为 .三、解答题(共8题,共66分)
-
17. 如图,正方形网格中(每个小正方形边长是1,小正方形的顶点叫做格点),△ABC的顶点均在格点上,请在所给的平面直角坐标系中解答下列问题:

⑴作出△ABC绕点C逆时针旋转90°后的;
⑵作出关于原点O成中心对称的 .
18. 如图,四边形ABCD是正方形.△ABE是等边三角形,M为对角线 BD(不含B,D点)上任意一点,将线段BM绕点B逆时针旋转60°得到BN,连接 EN,AM、CM.请判断线段 AM 和线段 EN 的数量关系,并说明理由. 19. 如图,把△ABC绕点B按逆时针方向旋转得到△DBE,已知点D、B、C在同一直线上,且∠ABE=∠D.
19. 如图,把△ABC绕点B按逆时针方向旋转得到△DBE,已知点D、B、C在同一直线上,且∠ABE=∠D.

求证:△ABC是等腰三角形.
20. 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°. (1)、将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)、将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.
(1)、将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)、将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.①在旋转的过程中,问运动几秒时,边MN恰好与射线OC平行;
②将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系(直接写出结果).
21. 如图, 线段 两端点坐标分别为 .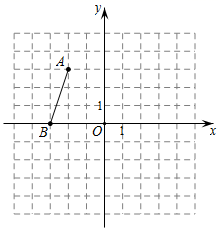 (1)、作出线段 绕点 逆时针旋转 后得到的线段 ;(2)、点 的坐标为 ,若线段 上有一点 , 则在线段 上的对应点 的 坐标为.(3)、若将线段 绕着某点旋转 恰好得到线段 , 点 与点 , 点 与点 是对应点,已知点 . 请通过无刻度的直尺画图找到旋转中心,将其标记为 .(保留作图痕迹)22. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)、作出线段 绕点 逆时针旋转 后得到的线段 ;(2)、点 的坐标为 ,若线段 上有一点 , 则在线段 上的对应点 的 坐标为.(3)、若将线段 绕着某点旋转 恰好得到线段 , 点 与点 , 点 与点 是对应点,已知点 . 请通过无刻度的直尺画图找到旋转中心,将其标记为 .(保留作图痕迹)22. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.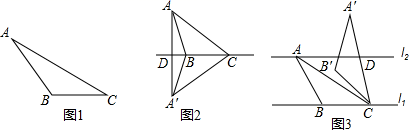 (1)、概念理解:
(1)、概念理解:如图1,在△ABC中,AC=6,DC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形.(填“是”或“否”)
(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连接AA'交直线BC于点D.若点B是△AA′C的重心,求 的值.
(3)、应用拓展:如图3,已知l1∥l2 , l1与l2之间的距离为2,“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B′C,A′C所在直线交l2于点D,直接写出CD的值.
23. 如图
如图1,圆 的两条弦 、 交于点 ,两条弦所成的锐角或者直角记为
(1)、点点同学通过画图和测量得到以下近似数据:的度数
的度数
的度数
猜想: 、 、 的度数之间的等量关系,并说明理由.
(2)、如图2,若 , , ,将 以圆心为中心顺时针旋转,直至点 与点 重合,同时 落在圆 上的点,连接 .①求弦 的长;
②求圆 的半径.
24. 如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的矩形ABEF.现将小矩形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α. (1)、当点D′恰好落在EF边上时,旋转角α=°;(2)、如图2,G为BC中点,且0°<α<90°,求证:GD′=DE′;(3)、小矩形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值,若不能,说明理由.
(1)、当点D′恰好落在EF边上时,旋转角α=°;(2)、如图2,G为BC中点,且0°<α<90°,求证:GD′=DE′;(3)、小矩形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值,若不能,说明理由.