2022-2023学年浙教版数学九上期中复习专题5 圆内接三角形、圆内接四边形、圆内接正多边形

试卷更新日期：2022-10-15 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 10个大小相同的正六边形按如图所示方式紧密排列在同一平面内， $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $O$ 均是正六边形的顶点.则点 $O$ 是下列哪个三角形的外心（）.

A、 $△ A E D$ B、 $△ A B D$ C、 $△ B C D$ D、 $△ A C D$

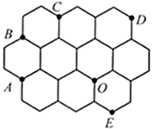查看试题解析
2. 根据已有的圆规作图痕迹，可用直尺成功找到三角形外心的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，D是等边△ABC外接圆 $\overset{⌢}{A C}$ 上的点，且∠CAD=20°，则∠ACD的度数为（）

A、20° B、30° C、40° D、45°

查看试题解析
4. 如图，A、B，C是⊙O上的点，且∠ACB＝140°．在这个图中，画出下列度数的圆周角：40°，50°，90°，140°，仅用无刻度的直尺能画出的有（）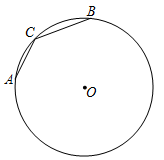

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，四边形ABCD是⊙O的内接四边形，∠ABC＝2∠D，∠AOB＝ $\frac{1}{3}$ ∠COB，⊙O的半径为 $\sqrt{3}$ ，连接AC交OB于点E，则图中阴影部分面积是（）

A、 $\frac{3 π}{4} - \frac{3}{2}$ B、 $\frac{\sqrt{3} π}{4} - \frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3} π}{4} - \sqrt{3}$ D、 $\frac{3 π}{4} - \frac{\sqrt{3}}{2}$

查看试题解析
6. 已知下列命题：
（ 1 ）抛物线y＝3x²+5x﹣1与两坐标轴交点的个数为2个；（2）相等的圆心角所对的弦相等；（3）任何正多边形都有且只有一个外接圆；（4）相似三角形的面积之比等于相似比的平方；（5）圆内接四边形对角相等；真命题的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，AB、AC分别为⊙O的内接正方形、内接正三边形的边，BC是圆内接n边形的一边，则n等于（）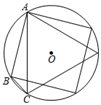

A、8 B、10 C、12 D、16

查看试题解析
8. 如图，正六边形ABCDEF与正方形BMEN均内接于⊙O，则 $\frac{B A}{B N}$ 的值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{2 \sqrt{2}}{3}$

查看试题解析
9. 下列关于正多边形的叙述，正确的是（　　）

A、正九边形既是轴对称图形又是中心对称图形 B、存在一个正多边形，它的外角和为720° C、任何正多边形都有一个外接圆 D、不存在每个外角都是对应每个内角两倍的正多边形

查看试题解析
10. 如图，点P是等边三角形ABC外接圆⊙O上的点，在以下判断中，不正确的是（）

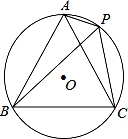A、当弦PB最长时，△APC是等腰三角形 B、当△APC是等腰三角形时，PO⊥AC C、当PO⊥AC时，∠ACP＝30° D、当∠ACP＝30°时，△BPC是直角三角形

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，在平面直角坐标系xOy中，点A的坐标为（0，7），点B的坐标为（0，3），点C的坐标为（3，0），那么△ABC的外接圆的圆心坐标为.

查看试题解析
12. 已知 $Rt △ A B C$ 中， $∠ C = 90^{\circ} ， A C = 5 ， B C = 12$ ，则 $△ A B C$ 的外接圆半径是

查看试题解析
13. 一个直角三角形的两条边长是方程x²﹣7x+12＝0的两个根，则此直角三角形的外接圆的直径为.

查看试题解析
14. 如图，四边形ABCD内接于⊙O，F是 $\overset{⌢}{C D}$ 上一点，且 $\overset{⌢}{D F} = \overset{⌢}{B C}$ ，连接CF并延长交AD的延长线于点E，连接AC.若∠ABC＝105°，∠BAC＝30°，则∠E的度数为度.

查看试题解析
15. 一条弦分圆周为4∶6，则这条弦所对的圆周角的度数为．

查看试题解析
16. 如图，已知正方形ABCD和正△EGF都内接于⊙O，当EF∥BC时， $\overset{⌢}{F B}$ 的度数为 .

查看试题解析

三、解答题（共8题，共66分）

17. 如图，四边形ABCD内接于⊙O，并且AD是⊙O的直径，C是 $\overset{⌢}{B D}$ 的中点，AB和DC的延长线交于⊙O外一点E，求证：BC＝EC.

查看试题解析
18. 如图，在“6×6”的正方形网格中，每个小正方形的边长均为1，已知△ABC的顶点均在小正方形的顶点上，按如下要求作三角形：（所作三角形的顶点在小正方形的顶点上）

(1)、在图1中作△ADB，使∠ADB=∠ACB；

(2)、在图2中作△AEB，使∠AEB=2∠ACB；

(3)、在图3中作△AFB，使∠AFB+∠ACB=180°．

查看试题解析
19. 某体育中心要修建一处公共服务设施，使它到三所运动员公寓A，B，C 的距离相等．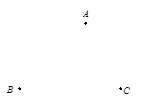

(1)、若三所运动员公寓A、B、C的位置如图所示，请你在图中确定这处公共服务设施（用点P表示）的位置；

(2)、若∠BAC＝90º，且AB=8，AC=6，求△ABC的外接圆的面积。

查看试题解析
20.
如图所示，正五边形ABCDE的对角线AC和BE相交于点M．

(1)、求证：AC∥DE．

(2)、求证：ME=AE．

查看试题解析
21. 如图，六边形ABCDEF是 $⊙ O$ 的内接正六边形.

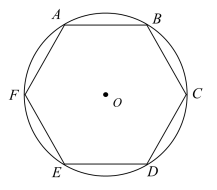(1)、求证：在六边形ABCDEF中，过顶点A的三条对角线四等分 $∠ B A F$ .

(2)、设 $⊙ O$ 的面积为 $S_{1}$ ，六边形ABCDEF的面积为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的值.

查看试题解析
22. 定义：若两个三角形中，有两组边对应相等且其中一组等边所对的角对应相等，但不是全等三角形，我们就称这两个三角形为偏等三角形．

(1)、如图1，点 $C$ 是弧 $B D$ 的中点， $∠ D A B$ 是弧 $B D$ 所对的圆周角， $A D > A B ，$ 连接 $A C$ 、 $D C 、 C B ，$ 试说明 $△ A C B$ 与 $△ A C D$ 是偏等三角形．

(2)、如图2， $△ A B C$ 与 $△ D E F$ 是偏等三角形，其中 $∠ A = ∠ D ， A C = D F ， B C = E F ，$ 猜想结论：一对偏等三角形中，一组等边的对角相等，另一组等边的对角．请填写结论，并说明理由．(以 $△ A B C$ 与 $△ D E F$ 为例说明)；

(3)、如图3， $△ A B C$ 内接于 $⊙ O ， A C = 6 ， ∠ A = 30 ° ， ∠ C = 45 ° ，$ 若点 $D$ 在 $⊙ O$ 上，且 $△ A D C$ 与 $△ A B C$ 是偏等三角形， $A D > C D ，$ 求 $A D$ 的值．

查看试题解析
23. 如图1，在⊙O中，弦AD平分圆周角∠BAC，我们将圆中以A为公共点的三条弦BA，CA，DA构成的图形称为圆中“爪形A”，弦BA，CA，DA称为“爪形A”的爪．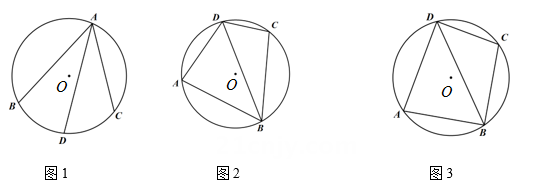

(1)、如图2，四边形ABCD内接于圆，AB＝BC，
①证明：圆中存在“爪形D”；
②若∠ADC＝120°，求证：AD＋CD＝BD

(2)、如图3，四边形ABCD内接于圆，其中BA＝BC，连接BD．若AD⊥DC，此时“爪形D”的爪之间满足怎样的数量关系，请直接写出结果．

查看试题解析
24. 综合与实践
“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.

提出问题：

如图1，在线段 $A C$ 同侧有两点B，D，连接 $A D$ ， $A B$ ， $B C$ ， $C D$ ，如果 $∠ B = ∠ D$ ，那么A，B，C，D四点在同一个圆上.

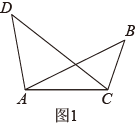
探究展示：

如图2，作经过点A，C，D的 $⊙ O$ ，在劣弧 $A C$ 上取一点E（不与A，C重合），连接 $A E$ ， $C E$ 则 $∠ A E C + ∠ D = 180 °$ （依据1）

$∵ ∠ B = ∠ D$

$∴ ∠ A E C + ∠ B = 180 °$

$∴$ 点A，B，C，E四点在同一个圆上（对角互补的四边形四个顶点共圆）

$∴$ 点B，D在点A，C，E所确定的 $⊙ O$ 上（依据2）

$∴$ 点A，B，C，E四点在同一个圆上

(1)、反思归纳：上述探究过程中的“依据1”、“依据2”分别是指什么？
依据1：；依据2：.

(2)、图3，在四边形 $A B C D$ 中， $∠ 1 = ∠ 2$ ， $∠ 3 = 45 °$ ，则 $∠ 4$ 的度数为.

(3)、展探究：如图4，已知 $△ A B C$ 是等腰三角形， $A B = A C$ ，点D在 $B C$ 上（不与 $B C$ 的中点重合），连接 $A D$ .作点C关于 $A D$ 的对称点E，连接 $E B$ 并延长交 $A D$ 的延长线于F，连接 $A E$ ， $D E$ .

①求证：A，D，B，E四点共圆；

②若 $A B = 2 \sqrt{2}$ ， $A D \cdot A F$ 的值是否会发生变化，若不变化，求出其值；若变化，请说明理由.

查看试题解析