2022-2023学年浙教版数学九上期中复习专题4 圆的基本性质
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列命题中不正确的是( )A、圆是轴对称图形,任何一条直径所在直线都是圆的对称轴 B、圆是中心对称图形,圆心是它的对称中心 C、图形经过旋转所得的对应点到旋转中心的距离相等 D、平分弦的直径一定垂直于这条弦2. 下列命题:①任意三点确定一个圆;②平分弦(不是直径)的直径垂直于弦;③相等的圆心角所对的弦相等;④长度相等的弧是等弧.其中真命题的有( )A、 个 B、 个 C、 个 D、 个3. 如图,在平面直角坐标系中,点A,C,N的坐标分别为(-2,0),(2,0),(4,3),以点C为圆心,2为半径画⊙C,点P在⊙C上运动,连接AP,交⊙C于点Q,点M为线段QP的中点,连接MN,则线段MN的最小值为( )
 A、 B、3 C、 D、4. 如图,已知在中,是直径, , 则下列结论不一定成立的是( )
A、 B、3 C、 D、4. 如图,已知在中,是直径, , 则下列结论不一定成立的是( )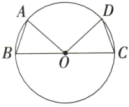 A、 B、 C、 D、到、的距离相等5. 如图,正方形ABCD内接于⊙O,若随意抛出一粒石子在这个圆面上,则石子落在正方形ABCD内概率是( )
A、 B、 C、 D、到、的距离相等5. 如图,正方形ABCD内接于⊙O,若随意抛出一粒石子在这个圆面上,则石子落在正方形ABCD内概率是( )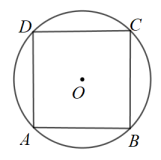 A、 B、 C、 D、6. 如图,点B,C,D在⊙A上, , ,则 的度数为( )
A、 B、 C、 D、6. 如图,点B,C,D在⊙A上, , ,则 的度数为( ) A、68° B、78° C、88° D、98°7. 如图,由边长为1的正方形组成的6×5网格中,一块含45°的三角板ABC的斜边AB始终经过格点N,AC始终经过格点M,点A在MN下方运动,格点P到A的距离最小值为( )
A、68° B、78° C、88° D、98°7. 如图,由边长为1的正方形组成的6×5网格中,一块含45°的三角板ABC的斜边AB始终经过格点N,AC始终经过格点M,点A在MN下方运动,格点P到A的距离最小值为( ) A、1 B、 C、 ﹣1 D、2 ﹣28. 如图,在半径为5的⊙ 中, , 是互相垂直的两条弦,垂足为 , ,则 的长为( )
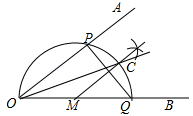
A、1 B、 C、 ﹣1 D、2 ﹣28. 如图,在半径为5的⊙ 中, , 是互相垂直的两条弦,垂足为 , ,则 的长为( ) A、3 B、4 C、 D、9. 已知∠AOB,作图.
A、3 B、4 C、 D、9. 已知∠AOB,作图.步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 于点C;
步骤3:画射线OC.
则下列判断:① = ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
 A、1 B、2 C、3 D、410. 如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是( )
A、1 B、2 C、3 D、410. 如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是( ) A、 B、 C、2- D、 -1
A、 B、 C、2- D、 -1二、填空题(每题4分,共24分)
-
11. 如图,点A,B,C是上的三个点,∠C=50°,则∠AOB=.
 12. 已知A为⊙O外一点,若点A到⊙O上的点的最短距离为2,最长距离为4,则⊙O的半径为 .13. 如图,在⊙O中, , AD⊥OC于点D,比较大小AB2AD.(填入“>”或“<”或“=”).
12. 已知A为⊙O外一点,若点A到⊙O上的点的最短距离为2,最长距离为4,则⊙O的半径为 .13. 如图,在⊙O中, , AD⊥OC于点D,比较大小AB2AD.(填入“>”或“<”或“=”). 14. 如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点 , , , 格点 , 的连线交于点 , 则的长为 .
14. 如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点 , , , 格点 , 的连线交于点 , 则的长为 . 15. 如图,是半圆的直径,是半圆的弦,沿弦折叠交直径于点.(1)当时,则的长为;(2)当 , 时,则的长为.
15. 如图,是半圆的直径,是半圆的弦,沿弦折叠交直径于点.(1)当时,则的长为;(2)当 , 时,则的长为.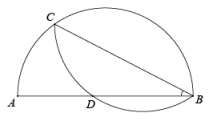 16. “一切为了U”是常山在赶考共同富裕道路上,最新确定的城市品牌.已知线段 , 对于坐标平面内的一个动点P,如果满足 , 则称点P为线段的“U点”,如图,二次函数与x轴交于点A和点B.(1)线段的长度为;(2)若线段的“U”点落在y轴的正半轴上,则该“U点”的坐标为 .
16. “一切为了U”是常山在赶考共同富裕道路上,最新确定的城市品牌.已知线段 , 对于坐标平面内的一个动点P,如果满足 , 则称点P为线段的“U点”,如图,二次函数与x轴交于点A和点B.(1)线段的长度为;(2)若线段的“U”点落在y轴的正半轴上,则该“U点”的坐标为 .
三、解答题(共8题,共66分)
-
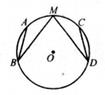
17. 如图,MB,MD是⊙O的两条弦,点A,C分别在 , 上,且AB=CD,M是 的中点.求证:MB=MD.
 18. 如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长.
18. 如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长. 19. 如图是一个以线段AB为直径的半圆,请按要求作图.(保留作图痕迹,不写作法)
19. 如图是一个以线段AB为直径的半圆,请按要求作图.(保留作图痕迹,不写作法)
( 1 )请用圆规和直尺作出圆心;
( 2 )请用圆规和直尺作出一个60°的角,使这个角的顶点在弧AB(A、B两点除外)上.
20. 在一个不透明的盒子里装有4个标有1,2,3,4的小球,它们形状、大小完全相同.小明从盒子里随机取出一个小球,记下球上的数字,作为点P的横坐标x,放回然后再随机取出一个小球,记下球上的数字,作为点P的纵坐标y.(1)、画树状图或列表,写出点P所有可能的坐标;(2)、求出点P在以原点为圆心,5为半径的圆上的概率.21. 将图中的破轮子复原,已知弧上三点A,B,C. (1)、用尺规作出该轮的圆心O,并保留作图痕迹;(2)、若△ABC是等腰三角形,设底边BC=8,腰AB=5,求该轮的半径R.22. 如图,在Rt△ABC中,∠ACB=90°,D为BC上一点,以AD为直径的⊙O经过点C,交AB于点E,且AC=AE,CF为⊙O的直径,连接FE并延长交BC于点G,连接AF。
(1)、用尺规作出该轮的圆心O,并保留作图痕迹;(2)、若△ABC是等腰三角形,设底边BC=8,腰AB=5,求该轮的半径R.22. 如图,在Rt△ABC中,∠ACB=90°,D为BC上一点,以AD为直径的⊙O经过点C,交AB于点E,且AC=AE,CF为⊙O的直径,连接FE并延长交BC于点G,连接AF。 (1)、求证:四边形ADGF是平行四边形;(2)、若AF:BC=3:8,BE=4,求⊙O的直径。23. 如图,四边形ABCD是⊙O 的内接四边形,对角线AC,BD交于点E,AB=AC.
(1)、求证:四边形ADGF是平行四边形;(2)、若AF:BC=3:8,BE=4,求⊙O的直径。23. 如图,四边形ABCD是⊙O 的内接四边形,对角线AC,BD交于点E,AB=AC. (1)、如图1,若BD是⊙O的直径,求证:∠BAC=2∠ACD;(2)、如图2,若BD⊥AC,DE =3,CE=4,求BE的长;(3)、如图3,若∠ABC+∠DCB=90°,AD=7,BC=24,求AB的长;(4)、在(3)的条件下,保持BC不动,使AD在⊙O上滑动,(滑动中AD长度保持不变)直接写出BD+AC的最大值.24. 已知P是 上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP.若 .
(1)、如图1,若BD是⊙O的直径,求证:∠BAC=2∠ACD;(2)、如图2,若BD⊥AC,DE =3,CE=4,求BE的长;(3)、如图3,若∠ABC+∠DCB=90°,AD=7,BC=24,求AB的长;(4)、在(3)的条件下,保持BC不动,使AD在⊙O上滑动,(滑动中AD长度保持不变)直接写出BD+AC的最大值.24. 已知P是 上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP.若 . (1)、如图1,当 , , 时,求 ⊙O 的半径;(2)、在(1)的条件下,求四边形APBQ的面积(3)、如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若 ,探究直线AB与ON的位置关系,并说明理由.
(1)、如图1,当 , , 时,求 ⊙O 的半径;(2)、在(1)的条件下,求四边形APBQ的面积(3)、如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若 ,探究直线AB与ON的位置关系,并说明理由.