2022-2023学年浙教版数学九上期中复习专题3 简单事件的概率
试卷更新日期：2022-10-15 类型：复习试卷
一、单选题（每题3分，共30分）
-
1. 下列事件是必然事件的是（ ）A、任意一个三角形，它的内角和等于180° B、打开电视机，正在播放广告 C、掷一枚硬币，正面朝上 D、明天太阳从西方升起2. 下列说法正确的是（ ）A、掷一枚质地均匀的骰子，掷得的点数为3的概率是 B、若AC、BD为菱形ABCD的对角线，则的概率为1 C、概率很小的事件不可能发生 D、通过少量重复试验，可以用频率估计概率3. 不透明袋中装有3个红球和5个绿球，这些球除颜色外无其他差别.从袋中随机摸出1个球是红球的概率为（ ）A、 B、 C、 D、4. 甲、乙两人各自掷一个普通的正方体骰子，如果两者之和为偶数，甲得1分；如果两者之和为奇数，乙得1分，此游戏（ ）A、是公平的 B、对乙有利 C、对甲有利 D、以上都不对5. 下列各选项的事件中，发生的可能性大小相等的是（ ）A、小明去某个路口，碰到红灯、黄灯和绿灯 B、任意抛掷一枚图钉，落地后钉尖“朝上”和“朝下” C、小亮在沿着Rt△ABC三边行走，他出现在AB，AC与BC边上 D、小红任意抛掷一枚均匀的骰子，朝上的点数为“偶数”和“奇数”6. 在如图所示的电路中，随机闭合开关S1、S2、S3中的两个，能让灯泡L1发光的概率是（ ）
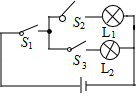A、 B、 C、 D、7. 在不透明的袋子中装有黑、白两种球共50个，这些球除颜色外都相同，随机从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则袋子中黑球的个数约为A、20个 B、30个 C、40个 D、50个8. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），为了了解该图案的面积是多少，我们采取了以下办法：用一个长为a，宽为b的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计实验结果），现将若干次有效实验的结果绘制成了如图②所示的折线统计图，由此估计不规则图案的面积大约是（ ）
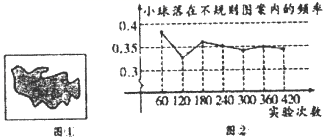A、a2 B、ab C、b2 D、ab9. 在大力发展现代化农业的形势下，现有 、 两种新玉米种子，为了了解它们的出芽情况，在推广前做了五次出芽实验，每次随机各自取相同种子数，在相同的培育环境中分别实验，实验情况记录如下：种子数量
100
300
500
1000
3000
出芽率
0.99
0.94
0.96
0.98
0.97
出芽率
0.99
0.95
0.94
0.97
0.96
下面有三个推断：
①当实验种子数量为100时，两种种子的出芽率均为0.99，所以 、 两种新玉米种子出芽的概率一样；
②随着实验种子数量的增加， 种子出芽率在0.97附近摆动，显示出一定的稳定性，可以估计A种子出芽的概率是0.97；
③在同样的地质环境下播种， 种子的出芽率可能会高于 种子．其中合理的是（ ）
A、①②③ B、①② C、①③ D、②③10. 不透明的袋子里有50张2022年北京冬奥会宣传卡片，卡片上印有会徽、吉祥物冰墩墩、吉祥物雪容融图案，每张卡片只有一种图案除图案不同外其余均相同，其中印有冰墩墩的卡片共有 张．从中随机摸出1张卡片，若印有冰墩墩图案的概率是 ，则 的值是（ ）A、250 B、10 C、5 D、1二、填空题（每题4分，共24分）
-
11. 转动如图所示的这些可以自由转动的转盘（转盘均被等分），当转盘停止转动后，根据“指针落在白色区域内”的可能性的大小，将转盘的序号按事件发生的可能性从小到大排列为 ．
12. 从2021年起，湖南普通高校招生考试实行“3+1+2”模式：“3”是指语文，数学，外语3科为必选科目，“1”是指在物理，历史2科中任选1科，“2”是指在化学，生物，思想政治，地理4科中任选2科.若小玲在“1”中选择了历史，在“2”中已选择了地理，则她选择生物的概率是.13. 如图：麻将是中国的国粹之一，玩法最为复杂有趣，是中国古人发明的一种博弈游戏．它开局拿牌要投两枚骰子，将两枚骰子的点数相加之和除以4看余数来决定是在哪家开始拿牌．余数为1则在自家拿牌，余数为2就在下家拿牌，余数为3则在对家拿牌，能被4整除就在上家拿牌，则在自家拿牌的概率为 ．
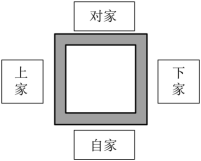14. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，实验数据如下表：摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.601
根据数据，估计袋中黑球有个．
15. 不透明的箱子里装有大小一样、黑白两种颜色的塑料球共5000个，为了估计两种颜色的球各有多少个，将箱子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回箱子中，多次重复上述过程后，发现摸到黑球的频率在0.7附近较稳定的波动，据此可以估计箱子里白球个数约是 个．16. 哥哥与弟弟玩一个游戏：三张大小、质地都相同的卡片上分别标有数字1，2，3，将标有数字的一面朝下，哥哥从中任意抽取一张，记下数字后放回洗匀，然后弟弟从中任意抽取一张，计算抽得的两个数字之和，如果和为奇数，则弟弟胜；和为偶数，则哥哥胜，该游戏对双方（填“公平”或“不公平”）．三、解答题（共8题，共66分）
-
17. 一个袋中有3张形状大小完全相同的卡片，编号为1、2、3，先任取一张，再从剩下的两张中任取一张.请你用列举法（画树状图或列表的方法）求取出的两张卡片上的数字之和为5的概率.18. 我区某中学就新冠疫情对青少年价值观产生的影响做了一个问卷调查，其中一项调查内容是：疫情期间出现的哪一个高频词汇最触动你的内心？A．生命，B．感恩，C．责任，D．奉献．每个同学只能从中选择一个“我最关注”的热词，如图是根据调查结果绘制的两幅不完整的统计图．请份根据统计图提供的信息，解答下列问题：
(1)、本次调查中，一共调查了名同学；(2)、扇形统计图中 ▲ ， 并补全条形统计图；(3)、从该校学生中随机抽取一个最关注热词“感恩”的学生的概率是多少．19. 如图①所示是一个正三棱锥（即正四面体）骰子的实物示意图，图②是它的立体示意图，它有四个面，各面分别标有数字5，4，4，7．
(1)、小康将这枚正三棱锥骰子随机抛掷一次，则掷得的数字是偶数的概率为 ．(2)、小齐随机抛掷两次骰子，试用列表法或画树状图法求两次掷得的数字和不小于11的概率．20. 2018年6月，湖州全面推进生活垃圾分类工作，如图是某小区放置的垃圾桶，从左到右依次是红色：有害垃圾；蓝色：可回收垃圾；绿色：厨余垃圾；黑色：其他垃圾．
(1)、居民A将一袋厨余垃圾随手放入一个垃圾桶，问他能正确投放垃圾的概率是 ．(2)、居民B手拎两袋垃圾，一袋是可回收垃圾，另一袋是有害垃圾，她先将可回收垃圾随手放入一个垃圾桶，然后把另一袋垃圾又随手放入其他垃圾桶．问：两袋垃圾都投放错误的概率？请画出树状图或列表说明理由．21. 有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，4，6；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球．小明先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），小刚再从瓶子中随机取出一个小球，记下小球上的数字．若得到的两数字之和是3的倍数，则小明赢；若得到的两数字之和是7的倍数，则小刚赢，你认为这个游戏公平吗？请说明理由．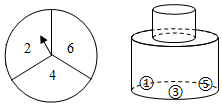
22. 在不透明的口袋中装有1个白色、1个红色和1个黄色的球（每个球除颜色外其余都相同）．(1)、如果从上述口袋中，同时随机摸出2个球，请用列表或画树状图的方法求摸到两球恰好是一白一黄的概率．(2)、小明往口袋中再放入若干个黄色的球（每个球除颜色外其余都相同），为了弄清黄球的个数，进行了摸球的实验（每次只摸一个，记录颜色后放回，搅匀后重复上述步骤），如表是实验的部分数据：请你估计：摸出一个球恰好是白球的概率大约是（精确到0.01），此时口袋中共有黄球约个．摸球次数
80
180
600
1000
1500
摸到白球次数
21
46
149
251
371
摸到白球的概率
0.2625
0.256
0.2483
0.251
0.247
23. 一个不透明的口袋中装有4个完全相同的小球，分别标有数字1，2，3，4，另外有一个可以自由旋转的圆盘，被分成面积相等的3个扇形区域，分别标有数字1，2，3（如图所示）．
(1)、从口袋中摸出一个小球，所摸球上的数字大于2的概率为 ；(2)、小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛，游戏规则为：一人从口袋中摸出一个小球，另一人转动圆盘，如果所摸球上的数字与圆盘上转出数字之和小于5，那么小龙去；否则小东去．你认为游戏公平吗？请用树状图或列表法说明理由．24. 在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)、从A、D、E、F四个点中任意取一点，以所取的这一点及点B、C为顶点画三角形，则所画三角形是等腰三角形的概率是；(2)、从A、D、E、F四个点中先后任意取两个不同的点，以所取的这两点及点B、C为顶点画四边形，求所画四边形是平行四边形的概率是多少？（用树状图或列表法求解）.