2022-2023学年浙教版数学九上期中复习专题2 二次函数的应用
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 在求解方程时,先在平面直角坐标系中画出函数的图象,观察图象与x轴的两个交点,这两个交点的横坐标可以看作是方程的近似解,分析右图中的信息,方程的近似解是( )
 A、 , B、 , C、 , D、 ,2. 汽车在刹车后,由于惯性作用还要继续向前滑行一段距离才能停下,我们称这段距离为“刹车距离”,刹车距离往往跟行驶速度有关,在一个限速35km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不妙,同时刹车,最后还是相撞了事发后,交警现场测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)的关系大致如下:S甲 ,S乙 .由此可以推测( )A、甲车超速 B、乙车超速 C、两车都超速 D、两车都未超速3. 一次函数与二次函数在同一平面直角坐标系中的图象可能是( )A、
A、 , B、 , C、 , D、 ,2. 汽车在刹车后,由于惯性作用还要继续向前滑行一段距离才能停下,我们称这段距离为“刹车距离”,刹车距离往往跟行驶速度有关,在一个限速35km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不妙,同时刹车,最后还是相撞了事发后,交警现场测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)的关系大致如下:S甲 ,S乙 .由此可以推测( )A、甲车超速 B、乙车超速 C、两车都超速 D、两车都未超速3. 一次函数与二次函数在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 4. 将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( )
4. 将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( ) A、或 B、或 C、或 D、或5. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
A、或 B、或 C、或 D、或5. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( ) A、193 B、194 C、195 D、1966. 某店销售一款运动服,每件进价100元,若按每件128元出售,每天可卖出100件,根据市场调查结果,若每件降价1元,则每天可多卖出5件,要使每天获得的利润最大,则每件需要降价( )A、3元 B、4元 C、5元 D、8元7. 喜迎国庆佳节,某商品原价400元,连续两次降价a%后售价为225元,下列所列方程中,正确的是( )A、400(1+a%)2=225 B、400(1-2a%)=225 C、400(1-a2%)=225 D、400(1-a%)2=2258. 如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A、193 B、194 C、195 D、1966. 某店销售一款运动服,每件进价100元,若按每件128元出售,每天可卖出100件,根据市场调查结果,若每件降价1元,则每天可多卖出5件,要使每天获得的利润最大,则每件需要降价( )A、3元 B、4元 C、5元 D、8元7. 喜迎国庆佳节,某商品原价400元,连续两次降价a%后售价为225元,下列所列方程中,正确的是( )A、400(1+a%)2=225 B、400(1-2a%)=225 C、400(1-a2%)=225 D、400(1-a%)2=2258. 如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( ) A、5米 B、4米 C、2.25米 D、1.25米9. 学校卫生间的洗手盘台面上有一瓶洗手液(如图①).小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是( )
A、5米 B、4米 C、2.25米 D、1.25米9. 学校卫生间的洗手盘台面上有一瓶洗手液(如图①).小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是( )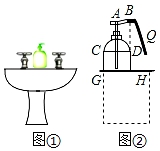 A、﹣ B、 C、﹣ D、10. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A、﹣ B、 C、﹣ D、10. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )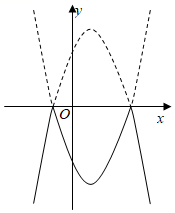 A、 或﹣2 B、 或﹣2 C、 或﹣3 D、 或﹣3
A、 或﹣2 B、 或﹣2 C、 或﹣3 D、 或﹣3二、填空题(每题4分,共24分)
-
11. 已知二次函数 自变量x与函数值y之间满足下列数量关系:
…
…
…
…
则代数式 的值是 .
12. 如图是二次函数y=-x2+bx+c的部分图象,若 ,则x的取值范围是.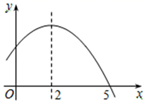 13. 将二次函数在轴下方的图象沿轴翻折到轴上方,图象的其余部分不变,得到一个新的图象,若直线与这个图象恰好有3个公共点,则的值为 .
13. 将二次函数在轴下方的图象沿轴翻折到轴上方,图象的其余部分不变,得到一个新的图象,若直线与这个图象恰好有3个公共点,则的值为 . 14. 如图,用长为16m的篱笆,一面利用墙(墙足够长)围成一块留有一扇1m宽的门的长方形花圃.设花圃的宽AB为xm,面积为ym2 , 则y与x的函数表达式为 .
14. 如图,用长为16m的篱笆,一面利用墙(墙足够长)围成一块留有一扇1m宽的门的长方形花圃.设花圃的宽AB为xm,面积为ym2 , 则y与x的函数表达式为 .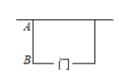 15. 如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式 . 已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.若球能越过球网,又不出边界,则h的取值范围为 .
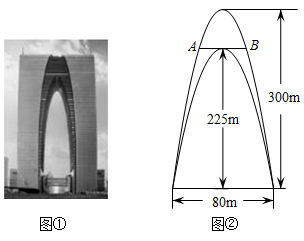
15. 如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式 . 已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.若球能越过球网,又不出边界,则h的取值范围为 . 16. 如图①,建筑“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体.如图②,“东方之门”的内侧轮廊是由两条抛物线组成的,已知其底部宽度均为80m,高度分别为300m和225m,则在内侧抛物线顶部处的外侧抛物线的水平宽度(AB的长)为
16. 如图①,建筑“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体.如图②,“东方之门”的内侧轮廊是由两条抛物线组成的,已知其底部宽度均为80m,高度分别为300m和225m,则在内侧抛物线顶部处的外侧抛物线的水平宽度(AB的长)为m.
三、解答题(共8题,共66分)
-
17. 如图二次函数的图象与x轴交于点、 , 根据图象解答下列问题:
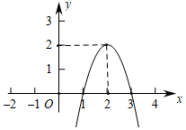 (1)、写出方程的两个根;(2)、当x为何值时,?当x为何值时,?(3)、写出y随x的增大而减小的自变量x的取值范围.18. 某商店在五一期间购进了600个旅游纪念品,进价每个6元,第一天以每个10元的价格售出了200个;第二天若以每个10元的价格仍可售出200个,但为了适当增加销量,决定降价销售,已知单价每降低1元,可多售出50个;第三天商店对剩下的旅游纪念品做清仓处理,以每个4元的价格全部售出.设第二天旅游纪念品单价降低x元 ,这批旅游纪念品的销售利润为y元(利润=售价-成本),请解决以下问题:(1)、用含x的代数式表示第三天的销售量(2)、若第三天销售量不超过前两天销售量之和的 ,求当第二天旅游纪念品的销售单价降低多少元时,这批旅游纪念品的销售总利润最大?最大值是多少?19. 一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:
(1)、写出方程的两个根;(2)、当x为何值时,?当x为何值时,?(3)、写出y随x的增大而减小的自变量x的取值范围.18. 某商店在五一期间购进了600个旅游纪念品,进价每个6元,第一天以每个10元的价格售出了200个;第二天若以每个10元的价格仍可售出200个,但为了适当增加销量,决定降价销售,已知单价每降低1元,可多售出50个;第三天商店对剩下的旅游纪念品做清仓处理,以每个4元的价格全部售出.设第二天旅游纪念品单价降低x元 ,这批旅游纪念品的销售利润为y元(利润=售价-成本),请解决以下问题:(1)、用含x的代数式表示第三天的销售量(2)、若第三天销售量不超过前两天销售量之和的 ,求当第二天旅游纪念品的销售单价降低多少元时,这批旅游纪念品的销售总利润最大?最大值是多少?19. 一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:x(元/件)
7
8
9
y(件)
8500
8000
7500
(1)、求y与x的函数关系式(不求自变量的取值范围);(2)、在销售过程中要求销售单价不低于成本价,且不高于17元/件,若某一周该商品的销售最不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)、抗疫期间,该商场这种商品售价不大于17元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.20. 如图所示,在△ABC中,∠B=90°,AB=5厘米,BC=7厘米.点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,当B点运动到C点时停止,P点也同时停止. (1)、如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积等于4平方厘米?(2)、如果点P,Q分别从点A,B同时出发,问第几秒时,四边形APQC的面积最小?其最小面积为多少?21. 如图,斜坡 长10米,按图中的直角坐标系可用 表示,点A,B分别在x轴和y轴上.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛线可用 表示.
(1)、如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积等于4平方厘米?(2)、如果点P,Q分别从点A,B同时出发,问第几秒时,四边形APQC的面积最小?其最小面积为多少?21. 如图,斜坡 长10米,按图中的直角坐标系可用 表示,点A,B分别在x轴和y轴上.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛线可用 表示. (1)、求抛物线的表达式及顶点坐标;(2)、在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?22. 如图,隧道的截面由抛物线和矩形构成,矩形的长为12m,宽为4m,按照如图所示建立平面直角坐标系,抛物线可以表示为
(1)、求抛物线的表达式及顶点坐标;(2)、在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?22. 如图,隧道的截面由抛物线和矩形构成,矩形的长为12m,宽为4m,按照如图所示建立平面直角坐标系,抛物线可以表示为 (1)、求抛物线的函数表达式,并计算出拱顶E到地面BC的距离;(2)、一辆货运汽车载一长方体集装箱后,高6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?(3)、在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?23. 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,其中点A的坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)、求抛物线的函数表达式,并计算出拱顶E到地面BC的距离;(2)、一辆货运汽车载一长方体集装箱后,高6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?(3)、在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?23. 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,其中点A的坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.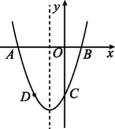 (1)、求抛物线的表达式;(2)、抛物线的对称轴上有一动点P,求△PAD周长的最小值;(3)、抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出点M的坐标.24. 如图1,皮皮小朋友燃放一种手持烟花,这种烟花每隔1.6秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同.皮皮小朋友发射出的第一发花弹的飞行高度h(米)随飞行时间t(秒)变化的规律如下表.
(1)、求抛物线的表达式;(2)、抛物线的对称轴上有一动点P,求△PAD周长的最小值;(3)、抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出点M的坐标.24. 如图1,皮皮小朋友燃放一种手持烟花,这种烟花每隔1.6秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同.皮皮小朋友发射出的第一发花弹的飞行高度h(米)随飞行时间t(秒)变化的规律如下表.t/秒
0
0.5
1
1.5
2
2.5
3
3.5
4
……
h/米
1.8
7.3
11.8
15.3
17.8
19.3
19.8
19.3
17.5
……
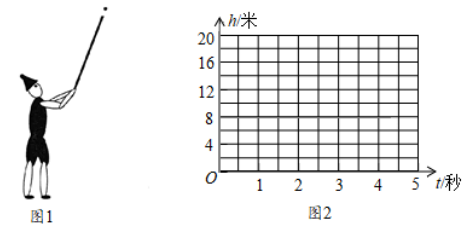 (1)、根据这些数据在图2的直角坐标系中画出相应的点,选择适当的函数表示h(米)与t(秒)之间的关系,并求出相应的函数表达式;(2)、当第一发花弹发射2秒后,第二发花弹达到的高度为多少米?(3)、为了安全,要求花弹爆炸时的高度不低于18米.皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求
(1)、根据这些数据在图2的直角坐标系中画出相应的点,选择适当的函数表示h(米)与t(秒)之间的关系,并求出相应的函数表达式;(2)、当第一发花弹发射2秒后,第二发花弹达到的高度为多少米?(3)、为了安全,要求花弹爆炸时的高度不低于18米.皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求