（人教版）2022-2023学年度第一学期九年级数学 中心对称 期中复习
试卷更新日期：2022-10-15 类型：复习试卷
一、单选题
-
1. 下列由箭头组成的图形中，不是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 下列图形分别是中国铁路、中国交建、中国航天、中国公路的标志，其中是中心对称图形的是（ ）A、
B、
C、
D、
4. 下列慈善公益图标中，是中心对称图形的是（ ）A、
B、
C、
D、
5. 下列图形中既是中心对称图形，又是轴对称图形的是（ ）A、
B、
C、
D、
6. 下列四个交通标志中，属于中心对称图形的是（ )A、
B、
C、
D、
7. 平面直角坐标系内与点P关于原点对称的点的坐标是（ ）A、 B、 C、 D、8. 已知点 ， 点关于原点的对称点是 ， 那么点的坐标是（ ）A、 B、 C、 D、9. 点 关于原点对称的点的坐标是（ ）A、 B、 C、 D、10. 在平面直角坐标系中，点P（4，﹣2）关于原点对称的点的坐标是（ ）A、（﹣4，2） B、（4，2） C、（﹣2，4） D、（﹣4，﹣2）二、填空题
-
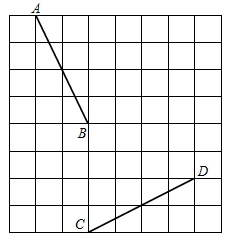
11. 在如图所示的网格中，每个小正方形的长度为1，点A的坐标为（﹣3，5），点B的坐标为（﹣1，1），点C的坐标为（﹣1，﹣3），点D的坐标为（3，﹣1），小强发现线段CD可以由线段AB绕着某点旋转一个角度得到，其中点A与点C对应，点B与点D对应，则这个旋转中心的坐标为 ．
12. 如图所示，已知抛物线C1 ， 抛物线C2 关于原点中心对称．如果抛物线C1 的解析式为y＝ (x＋2)2－1，那么抛物线C2的解析式为：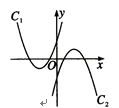
13. 在平行四边形、等边三角形、正方形、直角三角形这四类图形中，既是轴对称图形，又是中心对称图形的是 ．14. 点A（﹣2，﹣1）绕点B（﹣1，0）旋转180°得到点C．则点C坐标为 ．15. 如图，坐标原点O为菱形ABCD的中心，AD∥x轴，A点坐标为（﹣4，3），则B点坐标为 ．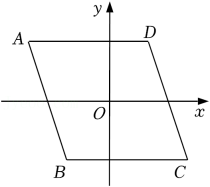
三、解答题
-
16. 如图，△ABC三个顶点的坐标分别是A(1，1)，B(4，2)，C(3，4).
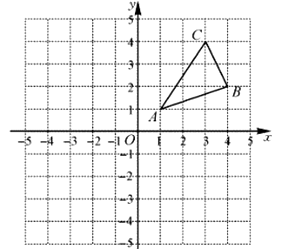(1)、请画出△ABC向左平移5个单位长度后得到的△A1B1C1；(2)、请画出△ABC关于原点对称的△A2B2C2；(3)、在x轴上求作一点P，使△PAB周长最小，请画出△PAB，并直接写出点P的坐标.17. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3）、B（﹣3，1）、C（﹣1，3）．
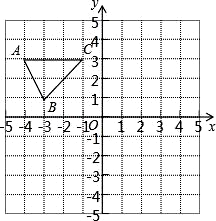(1)、请按下列要求画图：①将△ABC先向右平移4个单位长度、再向上平移2个单位长度，得到△A1B1C1 ， 画出△A1B1C1；
②△A2B2C2与△ABC关于原点O成中心对称，画出△A2B2C2 ．
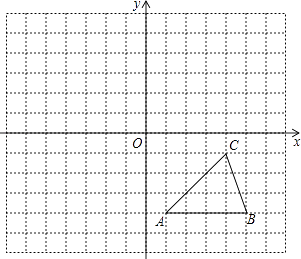
(2)、在（1）中所得的△A1B1C1和△A2B2C2关于点M成中心对称，请直接写出对称中心M点的坐标．18. 每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，①写出A、B、C的坐标．
②以原点O为对称中心，画出△ABC关于原点O对称的△A1B1C1 ， 并写出A1、B1、C1 ．
19. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
①若△ABC经过平移后得到△A1B1C1 ， 已知点C1的坐标为（4，0），写出顶点A1 ， B1的坐标；
②若△ABC和△A2B2C2关于原点O成中心对称图形，写出△A2B2C2的各顶点的坐标；
③将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 ， 写出△A3B3C3的各顶点的坐标．
20.如图，直线y=﹣x+4与x轴、y轴分别交于A、B两点，把△A0B绕点A顺时针旋转90°后得到△AO′B′，求点B′的坐标．
21. 已知|2﹣m|+（n+3）2=0，点P1、P2分别是点P（m，n）关于y轴和原点的对称点，求点P1、P2的坐标．22.如图所示，每个小正方形的边长为1个单位长度，作出△ABC关于原点对称的△A1B1C1并写出A1、B1、C1的坐标．
23. 如图，在平面直角坐标系中，点O为坐标原点，△AOB为顶点A，B的坐标分别为A（0，4），B（﹣3，0），按要求解答下列问题．
(1)、在图中，先将△AOB向上平移6个单位，再向右平移3个单位，画出平移后的△A1O1B1；（其中点A，O，B的对应点为A1 ， O1 ， B1）(2)、在图中，将△A1O1B1绕点O1顺时针旋转90°，画出旋转后的Rt△A2O1B2；（其中点A1 ， B1的对应点为A2 ， B2）(3)、直接写出点A2 ， B2的坐标．