(人教版)2022-2023学年度第一学期九年级数学 实际问题与二次函数 期中复习
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题
-
1. 如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
 A、5米 B、4米 C、2.25米 D、1.25米2. 如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是 , 则该运动员此次掷铅球的成绩是( )
A、5米 B、4米 C、2.25米 D、1.25米2. 如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是 , 则该运动员此次掷铅球的成绩是( )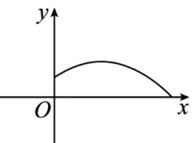 A、6m B、12m C、8m D、10m3. 如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= , tanβ= , 以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A、6m B、12m C、8m D、10m3. 如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= , tanβ= , 以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( ) A、 B、 C、 D、4. 用48米木料制作成一个如图所示的“目”形长方形大窗框(横档EF,GH也用木料).其中AB∥EF∥GH∥CD,要使窗框ABCD的面积最大,则AB的长为( )
A、 B、 C、 D、4. 用48米木料制作成一个如图所示的“目”形长方形大窗框(横档EF,GH也用木料).其中AB∥EF∥GH∥CD,要使窗框ABCD的面积最大,则AB的长为( ) A、6米 B、8米 C、12米 D、米5. 如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为 ,则小球从飞出到落地的所用时间为
A、6米 B、8米 C、12米 D、米5. 如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为 ,则小球从飞出到落地的所用时间为 A、 B、 C、 D、6. 小敏在某次投篮中,篮球的运动路线是抛物线 3.5的一部分(如图),若命中篮圈中心,则他与篮底的水平距离 是( )
A、 B、 C、 D、6. 小敏在某次投篮中,篮球的运动路线是抛物线 3.5的一部分(如图),若命中篮圈中心,则他与篮底的水平距离 是( ) A、3.5m B、3.8m C、4m D、4.5m7. 如图,函数 的图象与x轴交于A,B两点,点C是以 为圆心,2为半径的圆上的动点,P是 的中点,连结 ,则线段 的最小值是( )
A、3.5m B、3.8m C、4m D、4.5m7. 如图,函数 的图象与x轴交于A,B两点,点C是以 为圆心,2为半径的圆上的动点,P是 的中点,连结 ,则线段 的最小值是( ) A、1 B、 C、2 D、8. 有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A、1 B、 C、2 D、8. 有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( ) A、y= x2+ x B、y=- x2+ x C、y=- x2- x D、y=- x2+ x+169. 某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.则最大利润是( )
A、y= x2+ x B、y=- x2+ x C、y=- x2- x D、y=- x2+ x+169. 某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.则最大利润是( )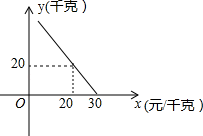 A、180 B、220 C、190 D、20010. 西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
A、180 B、220 C、190 D、20010. 西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为米,在如图所示的坐标系中,这个喷泉的函数关系式是( ) A、y=-(x-)2+3 B、y=-3(x+)2+3 C、y=-12(x-)2+3 D、y=-12(x+)2+3
A、y=-(x-)2+3 B、y=-3(x+)2+3 C、y=-12(x-)2+3 D、y=-12(x+)2+3二、填空题
-
11. 如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式 . 已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.若球能越过球网,又不出边界,则h的取值范围为 .
 12. 如图,若被击打的小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的关系为h=35t﹣5t2 , 则小球从飞出到落地所用时间为s.
12. 如图,若被击打的小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的关系为h=35t﹣5t2 , 则小球从飞出到落地所用时间为s.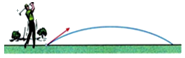 13. 如图,在平面直角坐标系中,抛物线与轴正半轴交于点 . 以为边在轴上方作正方形 , 延长交抛物线于点 , 再以为边向上作正方形 . 则点的坐标是 .
13. 如图,在平面直角坐标系中,抛物线与轴正半轴交于点 . 以为边在轴上方作正方形 , 延长交抛物线于点 , 再以为边向上作正方形 . 则点的坐标是 .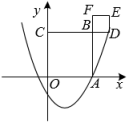 14. 如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升小时水位能由正常水位到达拱桥顶.
14. 如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就到达警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升小时水位能由正常水位到达拱桥顶. 15. 某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .
15. 某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .三、解答题
-
16. 现要用60米长的篱笆围成一个矩形场地(一边靠墙且墙长40米),应怎样围才能使矩形的面积S最大?最大是多少?
 17. 如图抛物线形拱桥,当拱顶离水面3m时,水面宽6m,连续降雨后,水面上涨1m,水面宽度减少多少?
17. 如图抛物线形拱桥,当拱顶离水面3m时,水面宽6m,连续降雨后,水面上涨1m,水面宽度减少多少? 18. 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,如果提高售价,请问将售价定每件为多少元时,才能在半月内获得最大利润?并求出最大利润.19. 某商场服装部销售一种名牌衬衫,平均每天可售出60件,每件盈利40元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价1元时,平均每天可多卖出2件.试说明每件衬衫降价多少元时,商场服装部每天盈利最多?最大盈利为多少元?20. 为促进经济发展,方便居民出行,某施工队要修建一个横断面为抛物线的公路隧道,隧道最高点P离路面 的距离为6米,宽度 为12米,隧道内设双向行车道,并且中间有一条宽为1米的隔离带.如果一货运汽车装载某大型设备后高为4米,宽为3.5米,按如图所示的平面直角坐标系这辆货车能否安全通过?为什么?
18. 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,如果提高售价,请问将售价定每件为多少元时,才能在半月内获得最大利润?并求出最大利润.19. 某商场服装部销售一种名牌衬衫,平均每天可售出60件,每件盈利40元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价1元时,平均每天可多卖出2件.试说明每件衬衫降价多少元时,商场服装部每天盈利最多?最大盈利为多少元?20. 为促进经济发展,方便居民出行,某施工队要修建一个横断面为抛物线的公路隧道,隧道最高点P离路面 的距离为6米,宽度 为12米,隧道内设双向行车道,并且中间有一条宽为1米的隔离带.如果一货运汽车装载某大型设备后高为4米,宽为3.5米,按如图所示的平面直角坐标系这辆货车能否安全通过?为什么? 21. 如图,一辆宽为2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),抛物线满足表达式y=﹣ x2+4.保证安全,车顶离隧道的顶部至少要有0.5米的距离,求货车的限高应是多少.
21. 如图,一辆宽为2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),抛物线满足表达式y=﹣ x2+4.保证安全,车顶离隧道的顶部至少要有0.5米的距离,求货车的限高应是多少.