2022-2023人教版数学八年级第一学期第十一章单元测试卷
试卷更新日期：2022-10-15 类型：单元试卷
一、单选题
-
1. 如图，在 中， ， ，则 的度数为（ ）
A、 B、 C、 D、2. 已知三角形中，某两条边的长分别为5和9，则另一条边的长可能是（ ）A、4 B、5 C、3 D、143. 内角和为540°的多边形是（ ）A、
B、
C、
D、
4. 一幅三角板，如图所示叠放在一起，则图中 的度数为（ ）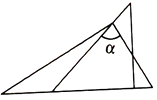
A、75° B、60° C、65° D、55°5. 下面四个图形中，能判断∠1＞∠2的是（ ）A、
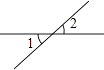B、
C、
D、
6. 如图，AB∥CD，且∠1=15°，∠2=35°+a，∠3=50°- a，∠4=30°- a，∠5=20°.则a的值为（ ）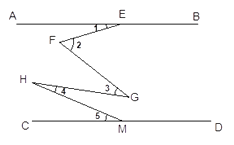
A、20° B、25° C、40° D、35°7. 如图，△ABC中，∠ACB=90°，D为AB上任一点，过D作AB的垂线，分别交边AC、BC的延长线于EF两点，∠BAC∠BFD的平分线交于点I，AI交DF于点M，FI交AC于点N，连接BI.下列结论：①∠BAC=∠BFD；②∠ENI=∠EMI；③AI⊥FI；④∠ABI=∠FBI；其中正确结论的个数是（ ）
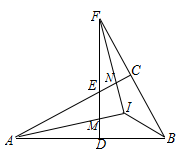A、1个 B、2个 C、3个 D、4个8. 一副三角板按如图放置，则下列结论：①如果∠2＝30°，则有AC//DE；②如果BC//AD，则有∠2＝45°；③∠BAE+∠CAD随着∠2的变化而变化；④如果∠4＝45°，那么∠1＝60°，其中正确的是（ ）
A、①②③ B、①②④ C、①③④ D、①②③④9. 如图，一张矩形纸片沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形），则∠OCD等于（ ）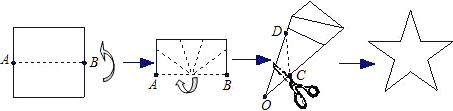
A、108° B、114° C、126° D、129°10. 如图，已知∠A＝60°，∠B＝40°，∠C＝30°，则∠D+∠E等于（ ）
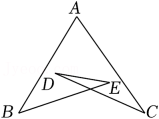A、30° B、40° C、50° D、60°二、填空题
-
11. 如图，在 中， 的平分线与 的平分线交于点D，过点D作BC的平行线交AB于点E，交AC于点F，已知 ，则 ．
12. 如图，AB∥CD，∠A=45゜，∠C=35゜，则∠D= ， ∠1= ．
13. 如图，在△ABC中，AD是△ABC的高，AE是△ABC的角平分线，已知∠BAC=82°，∠C=40°，则∠DAE= ．
14. 小明用剪刀将一块四边形纸板剪成了两个多边形，则这两个多边形内角的和为 ．15. 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时，就能拼成一个既不留空隙，又不相互重叠的平面图形，我们称之为镶嵌．用一种或几种正多边形镶嵌平面有多种方案，如：6个正三角形，记作（3，3，3，3，3，3）；3个正六边形，记作（6，6，6）；又如，（3，3，6，6）表示2个正三角形和2个正六边形的组合．请你再写出除了以上所举的三例以处的三种方案： ．16. 如图，已知 ，点 在 上，点 为平面内一点， ，过点 作 平分 平分 ，若 ，则 .
17. 如图，在边长为6的正方形ABCD中，点E、F、G分别在边AB、AD、CD上，EG与BF交于点I，AE=2，BF=EG，DG>AE，则DI的最小值为.
18. 已知一个包装盒的底面是内角和为720°的多边形，它是由另一个多边形纸片剪掉一个角以后得到的，则原多边形是边形．三、计算题
-
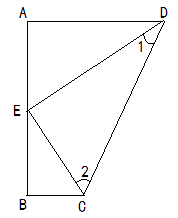
19. 如图所示，已知∠A=48°，∠D=25°，FD⊥BC于E，求∠B的度数．
20. 求出下列图中x的值。
21. 在平面直角坐标系xOy中描出下列两组点，分别将每组里的点用线段依次连接起来．第一组：A（﹣3，3）、C（4，3）；
第二组：D（﹣2，﹣1）、E（2，﹣1）．
(1)、直接写出线段AC与线段DE的位置关系；(2)、在（1）的条件下，线段AC，DE分别与y轴交于点B，F．若点M为射线OB上一动点（不与点O，B重合）．①当点M在线段OB上运动时，连接AM、DM，补全图形，用等式表示∠CAM、∠AMD、∠MDE之间的数量关系，并证明．
②当△ACM与△DEM面积相等时，求点M的坐标．
四、解答题
