2022-2023学年浙教版数学八上期中复习专题11一元一次不等式（组）

试卷更新日期：2022-10-15 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. $x = 1$ 是不等式 $x - b < 0$ 的一个解，则 $b$ 的值不可能是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 若关于x的不等式mx﹣n＞0的解集是x＜ $\frac{1}{5}$ ，则关于x的不等式（m+n）x＞n﹣m的解集是（　　）

A、x＜﹣ $\frac{2}{3}$ B、x＞﹣ $\frac{2}{3}$ C、x＜ $\frac{2}{3}$ D、x＞ $\frac{2}{3}$

查看试题解析
3. 在数学表达式： $- 3 < 0, 4 x + 3 y > 0, x = 3, x^{2} + 2 x y + y^{2}, x \neq 5, x + 2 > y + 3$ 中，是一元一次不等式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 不等式 $x - 1 < 0$ 的解在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
5. 不等式2x﹣6≤0的非负整数解的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 已知关于 $x$ 的不等式组 ${\begin{array}{l} x - a > 0 \\ 3 - 2 x > 0 \end{array}$ 的整数解共有3个，则 $a$ 的取值范围是（）

A、 $- 2 \leq a < - 1$ B、 $- 2 < a \leq 1$ C、 $- 2 < a < - 1$ D、 $- 2 \leq a \leq 1$

查看试题解析
7. 检测游泳池的水质，要求三次检验的pH的平均值不小于7.2，且不大于7.8.前两次检验，pH的读数分别是7.4，7.9，那么第三次检验的pH应该为多少才能合格?设第3次的pH值为x，由题意可得（）

A、7.2×3≤7.4+7.9+x≤7.8×3 B、7.2×3< 7.4+7.9+x≤7.8×3 C、7.2×3 >7.4+7.9+x>7.8×3 D、7.2×3< 7.4+7.9+x< 7.8×

查看试题解析
8. 关于 $x$ 的两个代数式 $x - 3$ 与 $x + 5$ 的值的符号相反，则 $x$ 的取值范围是（）

A、 $x > 3$ B、 $x < - 5$ C、 $- 5 < x < 3$ D、 $x < - 5$ 或 $x > 3$

查看试题解析
9. 不等式组 ${\begin{array}{l} 2 - x \leq 5 \\ \frac{x + 3}{2} < 1 \end{array}$ 的最大整数解是（）

A、﹣3 B、﹣2 C、﹣1 D、0

查看试题解析
10. 不等式组 ${\begin{array}{l} x + 2 > 1 \\ \frac{1}{2} x \leq 1 \end{array}$ 的解集在数轴上可表示为（）

A、 B、 C、 D、

查看试题解析

二、填空题（每题4分，共24分）

11. 某产品进价为每件200元，商店标价为每件300元.现商店准备将这批服装打折出售，但要保证毛利润不低于5%，则商店最低可按折出售.

查看试题解析
12. 不等式 $2 (x - 1) > - 1$ 的解为.

查看试题解析
13. 某电梯的额定限载量为1000千克，某人要用电梯把一批重物从底层搬到顶层，若人的身体质量为70千克，每箱货物质量为30千克，问他每次最多搬运多少箱？若设每次搬运货物x箱，则根据题意可列出关于x的不等式：．

查看试题解析
14. 如图是不等式组 $\{\begin{cases} x \geq a \\ x ＜ b \end{cases}$ 的解在数轴上的表示，则此不等式组的整数解是.

查看试题解析
15. 已知不等式组 ${\begin{array}{l} 2 x + 9 > - 6 x + 1 \\ x - k > 2 \end{array}$ 的解集为x＞﹣1，则k的取值范围是.

查看试题解析
16. 如图，用长为50米的铁丝一边靠墙围成两个长方形，墙的长度为40米，要使靠墙的一边不小于35 米，那么与墙垂直的一边AB的取值范围是.

查看试题解析

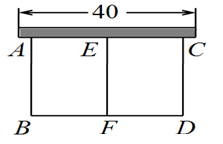
三、解答题（共8题，共66分）

17. 解下列不等式 (组)：

(1)、4x-1≥2x+4

(2)、 ${\begin{matrix} \frac{9 - 5 x}{2} \geq 3 x - 1 \\ 3 x - 3 \leq 5 x + 3 \end{matrix}$

查看试题解析
18.

(1)、解不等式：3x﹣2≤5x，并把解集在数轴上表示出来.

(2)、解不等式组 ${\begin{matrix} 2 (x - 2) \leq 3 - x \\ \frac{x + 1}{2} > \frac{x - 3}{3} + 1 \end{matrix}$ ，并写出它的最大整数解.

查看试题解析
19. 以下是圆圆解不等式组 ${\begin{array}{l} 2 (1 + x) > - 2 ① \\ - (1 - x) > 3 ② \end{array}$ 的解答过程：解：由①，得2+x＞﹣2，所以x＞﹣4．由②，得1﹣x＞﹣3，所以﹣x＞﹣2，所以x＞2．所以原不等式组的解是x＞2．圆圆的解答过程是否有错误？如果有错误，请写出正确的解答过程．

查看试题解析
20. 某业主贷款3.3万元购进一台机器，生产某种产品．已知产品的成本是每个3元，售价是每个5元，应付的税款和其它费用是售价的10%．若每个月能生产、销售6000个产品，问至少几个月后能赚回这台机器的贷款？（用列不等式的方法解决）．

查看试题解析
21. A、B两地相距200千米，早上8：00货车从A地出发将一批防疫物资运往B地，途中货车出现了故障.已知货车离开A地的路程y（km）与行驶时间x（h）的函数关系如图所示.

(1)、求货车出现故障前的速度；

(2)、若货车的司机经过24分钟维修排除了故障，继续运送物资赶往B地.应防疫需要，现要求该批次物资运到B地不迟于当天中午12：00，那么货车的速度至少应该提高到多少？

查看试题解析
22. 对 $x$ ， $y$ 定义一种新运算 $F (x ， y) = (a x + b y) (x + 3 y)$ （中 $a$ ， $b$ 均为非零常数）.例如： $F (1 ， 1) = 4 a + 4 b$ ；已知 $F (3 ， 1) = 0$ ， $F (0 ， 1) = - 9$ .

(1)、求 $a$ ， $b$ 的值；

(2)、若关于 $F$ 的不等式组 ${\begin{array}{l} F (3 t + 1 ， t) \geq k \\ F (6 t ， 1 - 2 t) < 27 \end{array}$ 恰好只有 $1$ 个整数解，求 $k$ 的取值范围.

查看试题解析
23. 接种新冠病毒疫苗，建立全民免疫屏障，是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心，据调查得知，2辆 $A$ 型冷链运输车与3辆 $B$ 型冷链运输车一次可以运输600盒：5辆 $A$ 型冷链运输车与6辆 $B$ 型冷链运输车一次可以运输1350盒.

(1)、求每辆 $A$ 型车和每辆 $B$ 型车一次可以分别运输多少盒疫苗.

(2)、计划用两种冷链运输车共12辆运输这批疫苗， $A$ 型车一次需费用5000元， $B$ 型车一次需费用3000元.若运输物资不少于1500盒，且总费用小于54000元.请你列出所有运输方案，并指出哪种方案所需费用最少，最少费用是多少？

查看试题解析
24. 某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体形状的无盖的纸盒．

(1)、现有正方形纸板162张，长方形纸板340张，若要做两种纸盒共100个，设竖式纸盒x个，需要长方形纸板张，正方形纸板张（请用含有x的式子）

(2)、在（1）的条件下，有哪几种生产方案？

(3)、若有正方形纸板162张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．已知290＜a＜300，求a的值．

查看试题解析