2022-2023学年浙教版数学八上期中复习专题8 直角三角形
试卷更新日期：2022-10-15 类型：复习试卷
一、单选题（每题3分，共30分）
-
1. 如图，在四边形ABCD中， ， ， ， ，则 的长为（ ）
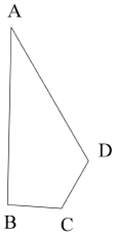A、2 B、1.5 C、3 D、2.52. 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=3，点D在AB上且AB=3AD，那么CD的长是（ ）
A、2 B、 C、2 D、43. 在Rt△ABC中，CD是斜边AB上的中线，则以下判断正确的是（ ）A、BC＝2CD B、CD＝2AB C、AC＝2CD D、CD＝BD4. 如图：BD⊥AC于点B，G是线段BD上一点(不与点B，点D重合)，且AB=BG，BD=BC，E，F分别为AD，CG的中点，AD=6，连结EF，DF，若△DEF为直角三角形，则DF的长度为（ ）
A、3 B、 C、3或 D、3或 或5. 如图，在△ABC中，∠ACB＝90°，D在BC上，E是AB的中点，AD、CE相交于F，且AD＝DB.若∠B＝20°，则∠DFE等于（ ）
A、30° B、40° C、50° D、60°6. 如图如果将一副三角板按如图方式叠放，那么 等于（ ）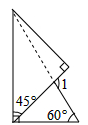
A、 B、 C、 D、7. 如图，在3×3的方格纸中，已知点A，B在方格顶点上（也称格点），若点C也是格点，且使得△ABC为直角三角形，则满足条件的C点有（ ）
A、1个 B、2个 C、3个 D、4个8. 如果直角三角形的两条直角边的长分别为6cm和8cm，那么斜边上的中线等于（ ）A、2.4cm B、4.8cm C、5cm D、10cm9. 如图，在 中， 是 延长线上一点， 是边 上一动点， 连结 ，作 与 关于 对称 (点 与点 对应)，连结 ，则 长的最小值是（ ）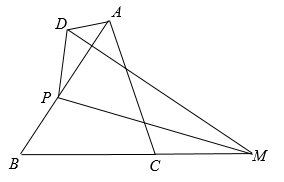
A、0.5 B、0.6 C、 D、10. 在△ABC中，∠BAC=90°，点D在边BC上，AD=AB （ ）
A、若AC=2AB，则∠C=30° B、若AC=2AB，则3BD=2CD C、若∠B=2∠C，则AC=2AB D、若∠B=2∠C，则S△ABD=2△ACD二、填空题（每题4分，共24分）
-
11. 在 中，锐角∠A＝25°，则另一个锐角∠B＝°.12. 如图，∠ABC＝30°，AB＝8，F是射线BC上一动点，D在线段AF上，以AD为腰作等腰直角三角形ADE（点A，D，E以逆时针方向排列），且AD＝DE＝1，连接EF，则EF的最小值为.
13. 如图∠MAN＝60°，若△ABC的顶点 B在射线AM上，且AB＝6，动点C从点A出发，以每秒1个单位沿射线AN运动，当运动时间 t是秒时，△ABC是直角三角形．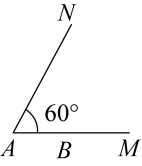
14. 如图，在直角三角形ABC中，∠ACB＝90°，AB＝7，点D是AB的中点，点P是斜边AB上的一个动点，FG是线段CP的垂直平分线，Q是FG上的一个动点，则PQ+QD的最小值为.
15. 直角三角形的两条直角边为6和8，则斜边上的中线长是 ．16. 在△ABC中，∠C=90°，∠A:∠B=1: 2，则∠B=.三、解答题（共8题，共66分）
-
17. 图l、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．点A和点B在小正方形的顶点上．
(1)、在图1中画出△ABC(点C在小正方形的顶点上)，使△ABC为直角三角形(画一个 即可)；(2)、在图2中画出△ABD(点D在小正方形的顶点上)，使△ABD为等腰三角形(画一个即可)；18. 如图，在中， ， ， 是边上的点，且 ， 过点作边的垂线交边于点 ， 求的长.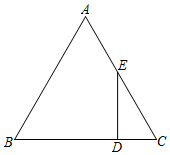
19. 如图，在△ABC中，∠B=∠C=60°，AD⊥BC于D，E为AC的中点，CB=8，求DE的长.
20. 如图，在△ABC中，AB＝AC，D是BC边的中点，过点D分别作DE、DF垂直AB、AC.
(1)、求证：DE＝DF；(2)、若∠B＝30°，AE＝1，求BC.21. 如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“奇妙三角形”．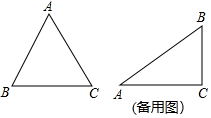
(1)、如图，在△ABC中，AB＝AC＝ ， BC＝4，求证：△ABC是“奇妙三角形”；(2)、在Rt△ABC中，∠C＝90°，AC＝ ， 若△ABC是“奇妙三角形”，求BC的长．22. 已知：如图，△ABC中，AC＝6，BC＝8，AB＝10，∠BCA的平分线与AB边的垂直平分线相交于点D，DE⊥AC，DF⊥BC，垂足分别是E、F.
(1)、求证：AE＝BF；(2)、求AE的长；(3)、求线段DG的长.23. 阅读下列材料，解决提出的问题：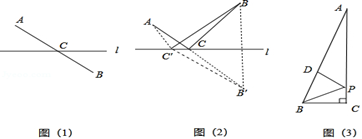
【最短路径问题】
如图（1），点A，B分别是直线l异侧的两个点，如何在直线l上找到一个点C，使得点C到点A，点B的距离和最短？我们只需连接AB，与直线l相交于一点，可知这个交点即为所求.
如图（2），如果点A，B分别是直线l同侧的两个点，如何在l上找到一个点C，使得这个点到点A、点B的距离和最短？我们可以利用轴对称的性质，作出点B关于的对称点B’，这时对于直线l上的任一点C，都保持CB＝CB’，从而把问题（2）变为问题（1）.因此，线段AB’与直线l的交点C的位置即为所求.
为了说明点C的位置即为所求，我们不妨在直线上另外任取一点C’，连接AC’，BC’，B’C’.
因为AB’≤AC’+C’B’ ， ∴AC+CB≤AC’+C’B，即AC+BC最小.
(1)、【数学思考】材料中划线部分的依据是.
(2)、材料中解决图（2）所示问题体现的数学思想是 .（填字母代号即可）A、转化思想 B、分类讨论思想 C、整体思想(3)、【迁移应用】如图3，在Rt△ABC中，∠C＝90°，∠BAC＝15°，点P为C边上的动点，点D为AB边上的动点，若AB＝6cm，求BP+DP的最小值.
24. 如果三角形的两个内角α与β满足2α+β＝90°，那么我们称这样的三角形为“准直角三角形”．
(1)、如图①，在Rt△ABC中，∠ACB＝90°，BD是△ABC的角平分线．求证：△ABD是“准直角三角形”．
(2)、关于“准直角三角形”，下列说法正确的是 （填写所有正确结论的序号）①在△ABC中，若∠A＝100°，∠B＝70°，∠C＝10°，则△ABC是准直角三角形；
②若△ABC是“准直角三角形”，∠C＞90°，∠A＝60°，则∠B＝20°；
③“准直角三角形”一定是钝角三角形．
(3)、如图②，B、C为直线l上两点，点A在直线l外，且∠ABC＝50°．若P是l上一点，且△ABP是“准直角三角形”，请直接写出∠APB的度数．