2022-2023学年浙教版数学八上期中复习专题7 等腰、等边三角形的性质与判定
试卷更新日期：2022-10-15 类型：复习试卷
一、单选题（每题3分，共30分）
-
1. 如图，为了让电线杆垂直于地面，工程人员的操作方法是：从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC，当固定点B，C到杆脚E的距离相等，且B，EC在同一直线上时，电线杆DE就垂直于BC工程人员这种操作方法的依据是（ ）
A、等边对等角 B、等角对等边 C、垂线段最短 D、等腰三角形“三线合一”2. 如图是一个6×6的正方形网格，每个小正方形的顶点都是格点，等腰△ABC的顶点都是图中的格点，其中点A、点B的位置如图所示，则点C可能的位置共有（ ）
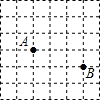A、10个 B、9个 C、8个 D、7个3. 如图，在△ABC中，∠B＝68°，∠C＝28°，分别以点A和点C为圆心，大于0.5AC的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（ ）
A、50° B、52° C、54° D、56°4. 已知等腰 中， 于点D，且 ，则 底角的度数为（ ）A、45°或75° B、60°或75° C、15°或75° D、45°或75°或15°5. 如图，在等腰 中， 是 内一点，过点 作三边 ， 的垂线段， 垂足分别为 ，若 ，则 两点间距离是（ ）
A、8 B、9 C、10 D、116. 下列说法正确的是（ ）A、顶角相等的两个等腰三角形全等 B、有一个角是60°的三角形是等边三角形 C、等腰三角形两底角相等 D、等腰三角形的高、中线、角平分线互相重合7. 如图，在ABC中，∠B＝50°，CD⊥AB于点D，∠BCD和∠BDC的角平分线相交于点E，F为边AC的中点，CD＝CF，则∠ACD+∠CED＝（ ）
A、125° B、145° C、175° D、190°8. 如图，在△ABC中，AD⊥BC，AB=AC，∠BAD=30°，AD=AE，则∠EDC=（ ）
A、 B、 C、 D、9. 如图，在△ABC中，ED∥BC，∠ABC和∠ACB的平分线分别交ED于点G、F，若FG＝3，ED＝6，则EB＋DC的值为（ ）
A、7 B、8 C、9 D、1010. 如图，在△ABC中，AD是∠BAC的平分线，EF∥AD，交AB于F，交CA延长线于G，下列说法正确的是（ ）
A、△ABD是等腰三角形 B、△AGF是等腰三角形 C、△BEF是等腰三角形 D、△ADC是等腰三角形二、填空题（每题4分，共24分）
-
11. 如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，路两旁50米内会受到噪音影响，已知有两台相距30米的拖拉机正沿ON方向行驶，它们的速度均为5米/秒，问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是秒.
12. 如图，根据尺规作图的痕迹，若 ，则 =度.
13. 由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小明设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可．如图1，衣架杆OA＝OB＝20cm，若衣架收拢时，∠AOB＝60°，如图2，则此时A，B两点之间的距离是cm．
14. 如图，在△ABC中，∠C=90°，∠B=30°，D是斜边AB的中点，P是边BC上的点，且PC=AC= ，以AP为边在AP右侧作等边 △APQ ，连结DQ，则DQ=；连结PD，则PD=。
15. 有一块直角三角形绿地，量得两直角边长为6 m，8 m.若现在要将绿地扩充成等腰三角形，且扩充时只能延长6 m的直角边，则扩充后等腰三角形绿地的面积为 m2.16. 如图1是一台手机支架，图2是其侧面示意图，AB、BC可分别绕点A、B转动，当AB、BC转动到∠BAE＝60°，∠ABC＝45°时，连结BE，∠ABE＝70°，延长BC交射线AE于D，AB不动，当BC绕点B顺时针转动度或逆时针转动度时，△BDE是等腰三角形.
三、解答题（共10题，共66分）
-
17. 已知等腰三角形一腰上的中线把这个三角形的周长分成15和16两部分，求这个等腰三角形的腰长和底边的长．18. 求证：等腰三角形底边中点到两腰的距离相等（要求画图，写出已知，求证，然后证明）.
已知：
求证：
证明：
19. 如图，在Rt△ABC中，∠A=90，∠B=30°，AC=2，D，E分别是BC和AB边的中点，在DA的延长线上取一点F，使AF=1．
(1)、求CE的长．(2)、求证：△CEF是等边三角形．20. 一艘轮船由西向东航行，在A处测得小岛P的方位是北偏东75°，又航行7海里后，在B处测得小岛P的方位是北偏东60°，若小岛周围3.8海里内有暗礁，问该船一直向东航行有无触礁的危险?
21. 如图，在等边△ABC中，点 ， 分别在边 ， 上， ， 过点作 ， 交的延长线于点 ， 若 ， 求的长．
22. 已知一个三角形的三条边的长分别为：n+6，3n，n+2(n为正整数)．若这个三角形是等腰三角形，求它的三边的长．23. 如图1，图2是两张形状、大小完全相同的“5×7”方格纸，方格纸中的每个小正方形的边长均为1，点A，B，C，D是方格纸上的四个格点（小正方形的顶点称为格点）．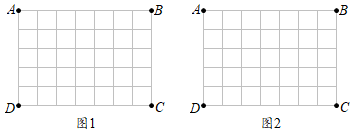
(1)、在图1中画一个等腰三角形ADE，其中点E在格点上，且不在线段AB或CD上（画一个即可）；(2)、在图2中画线段AM与BN，使AM=BN，其中点M，N分别是BC，CD上（不与端点重合）的格点．24. 如图，∠ACB＝90°，CD⊥AB于点D，AF平分∠CAB交CD于点E，交BC于点F，作EG∥AB交CB于点G．
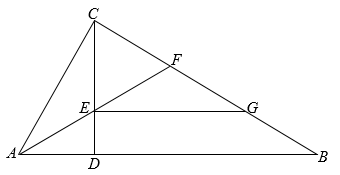(1)、求证：△CEF是等腰三角形；(2)、求证：CF＝BG；(3)、若F是CG的中点，EF＝1，求AB的长．25. 如图，在△ABC中，AB＝AC，点D在△ABC内，BD＝BC，∠DBC＝60°，点E在△ABC外，∠BCE＝150°，∠ABE＝60°．
(1)、求∠ADB的度数；(2)、判断△ABE的形状并证明；(3)、连接DE，若DE⊥BD，DE＝6，求AD的长．26. 如图，△ABC中，∠C=90°，AB=10cm，BC=6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．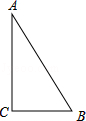
(1)、问t为何值时，△BCP为等腰三角形？(2)、另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？