2022-2023学年浙教版数学八上期中复习专题6 图形的轴对称
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 篆体是我国古代汉字书体之一,下列篆体字“复”,“兴”,“之”,“路”中,是轴对称图形的是( )A、
 B、
B、 C、
C、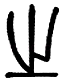 D、
D、 2. 下列科学防控“新冠肺炎”的图片中,是轴对称图形的是( )A、
2. 下列科学防控“新冠肺炎”的图片中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出,该球最后落入1号袋,经过反射的次数是( )
3. 如图,是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出,该球最后落入1号袋,经过反射的次数是( )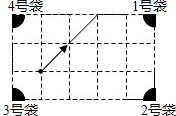 A、4次 B、5次 C、6次 D、7次4. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( )
A、4次 B、5次 C、6次 D、7次4. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( ) A、1个 B、2个 C、3个 D、4个5.
A、1个 B、2个 C、3个 D、4个5.用刻度尺分别画下列图形的对称轴,可以不用刻度尺上的刻度画的是( )
 A、①③④ B、②③ C、③④ D、①②6. 如图,正方形ABCD的边长为2,E是BC的中点,点P是AC边上的一个动点,连结BP,EP,则BP+EP的最小值为( )
A、①③④ B、②③ C、③④ D、①②6. 如图,正方形ABCD的边长为2,E是BC的中点,点P是AC边上的一个动点,连结BP,EP,则BP+EP的最小值为( ) A、 B、 C、 D、 +17. 如图,在△ABC中,点D在BC边上,点B关于直线AD的对称点B′落在AC的延长线上,若BC垂直平分AB′,则的值为( )
A、 B、 C、 D、 +17. 如图,在△ABC中,点D在BC边上,点B关于直线AD的对称点B′落在AC的延长线上,若BC垂直平分AB′,则的值为( ) A、 B、 C、 D、28. 如图,已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1 , O,P2三点所构成的三角形是( )
A、 B、 C、 D、28. 如图,已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1 , O,P2三点所构成的三角形是( ) A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形9. 如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )
A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形9. 如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )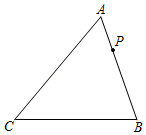 A、50° B、60° C、70° D、80°10. 某台球桌为如图所示的长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则AB:BC等于( )
A、50° B、60° C、70° D、80°10. 某台球桌为如图所示的长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则AB:BC等于( )
 A、1:2 B、2:3 C、2:5 D、3:5
A、1:2 B、2:3 C、2:5 D、3:5二、填空题(每题4分,共24分)
-
11. 等边三角形有条对称轴。12. 如图,等腰△BAC中,∠BAC=120°,BC=6,P为射线BA上的动点,M为BC上一动点,则PM+CP的最小值为 .
 13. 如图,在直角三角形ABC中,∠ACB=90° ,AB=7,点D是AB的中点,点P是斜边AB上的一个动点,FG是线段CP的垂直平分线,Q是FG上的一个动点,则PQ+QD的最小值为
13. 如图,在直角三角形ABC中,∠ACB=90° ,AB=7,点D是AB的中点,点P是斜边AB上的一个动点,FG是线段CP的垂直平分线,Q是FG上的一个动点,则PQ+QD的最小值为 14. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD边上任意两点,若△ABC的面积为24 ,则图中阴影部分的面积为。
14. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD边上任意两点,若△ABC的面积为24 ,则图中阴影部分的面积为。 15. 如图所示,在△ABC中,AB = 6 cm,AC = 3 cm,BC = 5 cm,点D,E分别在AC,AB上,且△BCD和△BED关于BD对称,则△ADE的周长为 cm.
15. 如图所示,在△ABC中,AB = 6 cm,AC = 3 cm,BC = 5 cm,点D,E分别在AC,AB上,且△BCD和△BED关于BD对称,则△ADE的周长为 cm.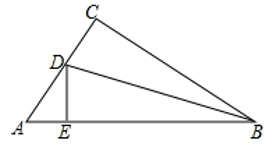 16. 如图,在四边形ABCD中,∠C=55°,∠B=∠D=90°,E,F分别是线段BC,DC上的动点,当 周长最小时,∠EAF的度数为.
16. 如图,在四边形ABCD中,∠C=55°,∠B=∠D=90°,E,F分别是线段BC,DC上的动点,当 周长最小时,∠EAF的度数为.
三、作图题(共3题,共18分)
-
17. 在4×4的方格中有五个同样大小的正方形如图摆放,请分别在甲、乙、丙三个图中添加一个正方形到空白方格中,使它与其余五个正方形组成的新图形是一个轴对称图形,并画出图形.
 18. 如图,已知△ABC的三个顶点在格点上.
18. 如图,已知△ABC的三个顶点在格点上.
 (1)、作出与△ABC关于y轴对称的图形△A1B1C1;(2)、写出△ABC关于x轴对称的△A2B2C2的三个顶点坐标;(3)、求△ABC的面积.19. 如图,在平面直角坐标系中,A(﹣3,3),B(﹣4,4),C(0,﹣1).
(1)、作出与△ABC关于y轴对称的图形△A1B1C1;(2)、写出△ABC关于x轴对称的△A2B2C2的三个顶点坐标;(3)、求△ABC的面积.19. 如图,在平面直角坐标系中,A(﹣3,3),B(﹣4,4),C(0,﹣1).
⑴在图中作出△ABC关于y轴对称的△A1B1C1 , 并写出△A1B1C1顶点的坐标;
⑵求△ABC的周长;
⑶在x轴上求出点P坐标,使PB+PC最小.
四、解答题(共5题,共48分)
-
20. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
 (1)、在图中画出与△ABC关于直线
(1)、在图中画出与△ABC关于直线 成轴对称的△AB′C′; (2)、线段
成轴对称的△AB′C′; (2)、线段 被直线
被直线  ; (3)、在直线
; (3)、在直线 上找一点P,使PB+PC的长最短,并算出这个最短长度。 21. 如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元.
上找一点P,使PB+PC的长最短,并算出这个最短长度。 21. 如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元. (1)、请在河流上选择水厂的位置M,使铺设水管的费用最少.(不写作法,保留作图痕迹)(2)、最低费用为多少?22. 已知Rt△ABC中∠C=90°,且BC=9,∠B=30°.
(1)、请在河流上选择水厂的位置M,使铺设水管的费用最少.(不写作法,保留作图痕迹)(2)、最低费用为多少?22. 已知Rt△ABC中∠C=90°,且BC=9,∠B=30°.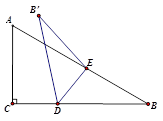


图1 图2 图3
(1)、如图1、2,若点D是CB上一点,且CD=3,点E是AB上的动点,将△DBE沿DE对折,点B的对应点为B’(点B’和点C在直线AB的异侧),DB’与AB交于点H.①当∠B’EA=20°时,求∠EDB的度数.
②当△B’HE是等腰三角形时,求∠DEB的度数.
(2)、如图2,若点D是CB上一点,且CD=3,M是线段AC上的动点,以∠MDN为直角构造等腰直角△DMN(D,M,N三点顺时针方向排列),在点M的运动过程中,直接写出CN+NB的最小值.23. 如图,已知在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,点D是边AB上的一个动点. (1)、当D为AB中点时,求CD的长;(2)、当BD=CD时,求证:D为AB中点;(3)、作A关于CD的对称点A'.
(1)、当D为AB中点时,求CD的长;(2)、当BD=CD时,求证:D为AB中点;(3)、作A关于CD的对称点A'.①当A'落在BC边上时,求△A'BD的面积;
②当A'D与△ABC某一条边平行时,则AD的长为 ▲ .(直接写出答案
24. 如图
 (1)、性质:角平分线上的点到角两边的距离相等,如图1:OP平分∠MON,PC⊥OM于C,PB⊥ON于B,则PBPC(填“ ”“ ”或“=”);(2)、探索:如图2,小明发现,在△ABC中,AD是∠BAC的平分线,则 ,请帮小明说明原因.(3)、应用:如图3,在小区三条交叉的道路AB,BC,CA上各建一个菜鸟驿站D,P,E,工作人员每天来回的路径为P→D→E→P,
(1)、性质:角平分线上的点到角两边的距离相等,如图1:OP平分∠MON,PC⊥OM于C,PB⊥ON于B,则PBPC(填“ ”“ ”或“=”);(2)、探索:如图2,小明发现,在△ABC中,AD是∠BAC的平分线,则 ,请帮小明说明原因.(3)、应用:如图3,在小区三条交叉的道路AB,BC,CA上各建一个菜鸟驿站D,P,E,工作人员每天来回的路径为P→D→E→P,①问点P应选在BC的何处时,才能使PD+DE+PE最小?
②若∠BAC=30°,S△ABC=10,BC=5,则PD+DE+PE的最小值是多少?