2022-2023学年浙教版数学八上期中复习专题5 角平分线、线段垂直平分线与尺规作图
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题(每题2分,共20分)
-
1. 下列尺规作图,能判断AD是△ABC边上的中线的是( )A、
 B、
B、 C、
C、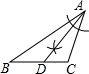 D、
D、 2. 如图是作△ABC的作图痕迹,则此作图的已知条件是( )
2. 如图是作△ABC的作图痕迹,则此作图的已知条件是( ) A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角3. 学习了角平分线及其性质后,某校数学兴趣小组的同学尝试只用一副带刻度的三角板作的角平分线,根据提供的条件,无法判断是角平分线的是( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角3. 学习了角平分线及其性质后,某校数学兴趣小组的同学尝试只用一副带刻度的三角板作的角平分线,根据提供的条件,无法判断是角平分线的是( ) A、 , P为中点 B、 , C、 , D、 , P为中点4. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
A、 , P为中点 B、 , C、 , D、 , P为中点4. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( ) A、①② B、①③ C、②③ D、①②③5. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N , 使OM=ON , 再分别过点M、N作OA、OB的垂线,交点为P , 画射线OP . 可证得△POM≌△PON , OP平分∠AOB . 以上依画法证明△POM≌△PON根据的是( )
A、①② B、①③ C、②③ D、①②③5. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N , 使OM=ON , 再分别过点M、N作OA、OB的垂线,交点为P , 画射线OP . 可证得△POM≌△PON , OP平分∠AOB . 以上依画法证明△POM≌△PON根据的是( ) A、SSS B、HL C、AAS D、SAS6. 如图,△ABC中,AC<BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( )
A、SSS B、HL C、AAS D、SAS6. 如图,△ABC中,AC<BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( ) A、
A、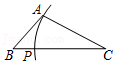 B、
B、 C、
C、 D、
D、 7. 已知∠AOB,在射线OA,OB上分别截取OD=OE,分别以点D,E为圆心,以大于 DE且同样长为半径画弧,在∠AOB内两弧交于点C,作射线OC,OC就是∠AOB的角平分线.作图依据是( )A、SAS B、ASA C、SSS D、HL8. 如图,已知∠AOB,按下面步骤作图:
7. 已知∠AOB,在射线OA,OB上分别截取OD=OE,分别以点D,E为圆心,以大于 DE且同样长为半径画弧,在∠AOB内两弧交于点C,作射线OC,OC就是∠AOB的角平分线.作图依据是( )A、SAS B、ASA C、SSS D、HL8. 如图,已知∠AOB,按下面步骤作图:
(1)在射线OA上任意取一点C,以点O为圆心,OC长为半径作弧MN,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,两弧在∠AOB内部交于点E,连接CE,DE;
(3)作射线OE交CD于点F.根据以上所作图形,有如下结论:①CE∥OB;②CE=2CF;③∠AOE=∠BOE;④CD⊥OE.其中正确的有( )
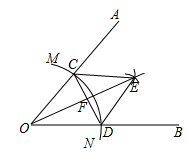
A、①②③④ B、②③ C、③④ D、②③④9. 已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )A、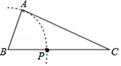 B、
B、 C、
C、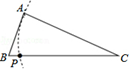 D、
D、 10. 如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为( )
10. 如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为( ) A、3 B、4 C、6 D、7
A、3 B、4 C、6 D、7二、填空题(每空2分,共12分)
-
11. 如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 .
 12. 如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC。由这种作图方法得到的△D′O′C′和△DOC全等的依据是(写出全等判定方法的简写).
12. 如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC。由这种作图方法得到的△D′O′C′和△DOC全等的依据是(写出全等判定方法的简写).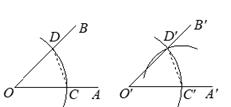 13. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.
13. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.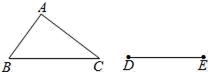 14. 已知,在△ABC中,∠A>∠B,分别以点A,C为圆心,大于 AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A= .
14. 已知,在△ABC中,∠A>∠B,分别以点A,C为圆心,大于 AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A= . 15. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .16. 如图,已知线段AB,分别以A、B为圆心,大于AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC,E为AC的中点,连接DE,当线段AB=4,∠ACB=60°时,△CED周长是
15. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .16. 如图,已知线段AB,分别以A、B为圆心,大于AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC,E为AC的中点,连接DE,当线段AB=4,∠ACB=60°时,△CED周长是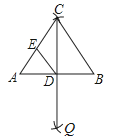
三、解答题(共12题,共88分)
-
17. 如图,在9×4的方格纸ABCD中,每个小正方形的边长均为1,点E为格点(注:小正方形顶点称为格点).请仅用无刻度直尺按要求画图.

⑴在CD边上找一点P,连结AP,使△AEP是等腰三角形;
⑵在AB边上找一点Q,使EQ⊥AP,画出线段EQ.
18. 如图,在4x4的方格纸中,请按要求画格点三角形(顶点在格点上).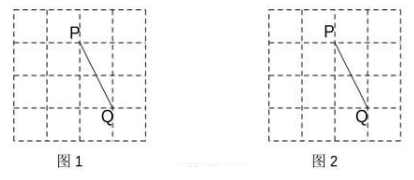 (1)、在图1中画格点△PQO,使△PQO是以点P为直角顶点的等腰直角三角形.(2)、在图2中画格点△QMN,使PQ是△QMN 的中线,且M,N不在同一条网格线上.19. 如图,已知线段 , .
(1)、在图1中画格点△PQO,使△PQO是以点P为直角顶点的等腰直角三角形.(2)、在图2中画格点△QMN,使PQ是△QMN 的中线,且M,N不在同一条网格线上.19. 如图,已知线段 , . (1)、尺规作图:作等腰 , 使底边长为 , 上的高为.(2)、若 , , 求的周长.20. 如图,在正方形网格中,画格点三角形(顶点是网格线的交点的三角形)ABC,满足以下条件:
(1)、尺规作图:作等腰 , 使底边长为 , 上的高为.(2)、若 , , 求的周长.20. 如图,在正方形网格中,画格点三角形(顶点是网格线的交点的三角形)ABC,满足以下条件: (1)、在图1中画格点△ABC,使△ABC是等腰三角形,且BC=AB;(2)、在图2中画格点△ABC,使△ABC是直角三角形,且BC=2AB.
(1)、在图1中画格点△ABC,使△ABC是等腰三角形,且BC=AB;(2)、在图2中画格点△ABC,使△ABC是直角三角形,且BC=2AB.
21. 如图,在一条东西向的马路上有广场A和医院C,在各自正北方向上分别有汽车站B和汽车站D,已知AC=14km,AB=4km,CD=8km.,市政府打算在马路AC段之间建造一个加油站P.

图1 图2
(1)、若要使得加油站P到两汽车站的距离之和最小,请用尺规作图在图1中作出加油站P的位置,并直接写出此时的最小值. (作图请保留痕迹,结果可以保留根号)(2)、若要使得加油站到两汽车站的距离相等,请用尺规作图在图2中作出加油站P的位置,并求出此时PA的距离.(作图请保留痕迹)22. 已知△ABC(如图),根据要求作图.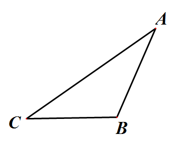
( 1 )用直尺和圆规作BC边上的中线;
( 2 )用直尺和圆规作∠ACB的平分线;
( 3 )作BC边上的高线
23. 如图,在方格中,按下列要求画三角形,使它的顶点均在方格的顶点上(小正方形边长为 ) (1)、在图1中画一个三角形与 全等,且有一条公共边;(2)、在图2中画一个面积为 的等腰直角三角形.24. 已知:两边及其夹角,线段 , , .
(1)、在图1中画一个三角形与 全等,且有一条公共边;(2)、在图2中画一个面积为 的等腰直角三角形.24. 已知:两边及其夹角,线段 , , .求作: ,使 , ,(用尺规作图,保留作图痕迹,不写作法).
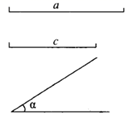
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的 是唯一的,依据是三角形全等判定定理中的_▲_.
25. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E,交BA的延长线于F. (1)、求证:△ABD≌△ACF;(2)、若BD平分∠ABC,求证:CE= BD;(3)、若D为AC上一动点,∠AED如何变化?若变化,求它的变化范围;若不变,求出它的度数,并说明理由.26. 如图,△ABC中,AB=AC ,
(1)、求证:△ABD≌△ACF;(2)、若BD平分∠ABC,求证:CE= BD;(3)、若D为AC上一动点,∠AED如何变化?若变化,求它的变化范围;若不变,求出它的度数,并说明理由.26. 如图,△ABC中,AB=AC ,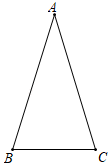 (1)、请你利用直尺和圆规完成如下操作:
(1)、请你利用直尺和圆规完成如下操作:①作△ABC的角平分线AD;
②作边AB的垂直平分线EF , EF与AD相交于点P;
③连接PB , PC .
请你观察图形解答下列问题:
(2)、写出线段PA , PB , PC之间的数量关系;请说明理由.(3)、若∠ABC=70°,求∠BPC的度数.27. 在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,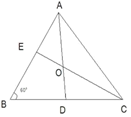 (1)、求∠AOC的度数(2)、连接BO,试说明BO平分∠ABC(3)、判断AC、AE、CD的关系,并说明理由.28. 如图
(1)、求∠AOC的度数(2)、连接BO,试说明BO平分∠ABC(3)、判断AC、AE、CD的关系,并说明理由.28. 如图 (1)、尺规作图1:
(1)、尺规作图1:已知:如图,线段AB和直线且点B在直线上
求作:点C,使点C在直线上并且使△ABC为等腰三角形.
作图要求:保留作图痕迹,不写作法,做出所有符合条件的点C.
(2)、特例思考:如图一,当∠1=90°时,符合(1)中条件的点C有个;如图二,当∠1=60°时,符合(1)中条件的点C有个.
(3)、拓展应用:如图,∠AOB=45°,点M,N在射线OA上,OM=x,ON=x+2,点P是射线OB上的点.若使点P,M,N构成等腰三角形的点P有且只有三个,求x的值.