2022-2023学年浙教版数学八上期中复习专题4 三角形全等的性质与判定
试卷更新日期:2022-10-15 类型:复习试卷
一、单选(每题2分,共24分)
-
1. 下列图形是全等图形的是( )A、
 B、
B、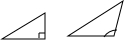 C、
C、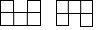 D、
D、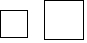 2. 如图, ,点 在同一条直线上, ,则 的长是( )
2. 如图, ,点 在同一条直线上, ,则 的长是( ) A、4.5 B、5 C、5.5 D、63. 已知图中的两个三角形全等,则∠α等于( )
A、4.5 B、5 C、5.5 D、63. 已知图中的两个三角形全等,则∠α等于( ) A、50° B、60° C、70° D、80°4. 某实验室有一块三角形玻璃,被摔成如图所示的四块,胡老师想去店里买一块形状、大小与原来一样的玻璃,胡老师要带的玻璃编号是( )
A、50° B、60° C、70° D、80°4. 某实验室有一块三角形玻璃,被摔成如图所示的四块,胡老师想去店里买一块形状、大小与原来一样的玻璃,胡老师要带的玻璃编号是( )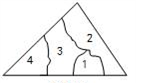 A、1 B、2 C、3 D、45. 如图,△ABC≌△DEF,BC=12,EC=7,则CF的长为( )
A、1 B、2 C、3 D、45. 如图,△ABC≌△DEF,BC=12,EC=7,则CF的长为( ) A、5 B、6 C、7 D、86. 如图,已知△OAB≌△OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是( )
A、5 B、6 C、7 D、86. 如图,已知△OAB≌△OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是( ) A、∠BDO=62° B、∠BOC=21° C、CD∥OA D、OC=47. 下列命题是假命题的是( )A、等底等高的两个三角形面积相等 B、两个全等三角形的面积相等 C、面积相等的两个三角形全等 D、等腰三角形底边上的高线和中线互相重合8. 如图,BP平分∠ABC,D为BP上一点,点E,F分别在BA,BC上,且满足DE=DF.若∠BED=140°,则∠BFD的度数是( )
A、∠BDO=62° B、∠BOC=21° C、CD∥OA D、OC=47. 下列命题是假命题的是( )A、等底等高的两个三角形面积相等 B、两个全等三角形的面积相等 C、面积相等的两个三角形全等 D、等腰三角形底边上的高线和中线互相重合8. 如图,BP平分∠ABC,D为BP上一点,点E,F分别在BA,BC上,且满足DE=DF.若∠BED=140°,则∠BFD的度数是( )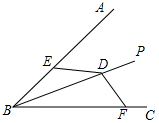 A、40° B、50° C、60° D、70°9. 如图,在OA,OB上分别截取OD,OE使OD=OE,再分别以点D、E为圆心,大于 DE长为半径作弧,两弧在∠AOB内交于点C,射线OC就是∠AOB的角平分线.理由是连结CD,CE,证△COD≌△COE得∠COD=∠COE.证△COD≌△COE的条件是( )
A、40° B、50° C、60° D、70°9. 如图,在OA,OB上分别截取OD,OE使OD=OE,再分别以点D、E为圆心,大于 DE长为半径作弧,两弧在∠AOB内交于点C,射线OC就是∠AOB的角平分线.理由是连结CD,CE,证△COD≌△COE得∠COD=∠COE.证△COD≌△COE的条件是( ) A、SAS B、AAS C、ASA D、SSS10. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( )
A、SAS B、AAS C、ASA D、SSS10. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( ) A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E11. 如图,已知 ,添加一个条件,使得 ≌ ,下列条件添加错误的是( )
A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E11. 如图,已知 ,添加一个条件,使得 ≌ ,下列条件添加错误的是( ) A、 B、 C、 D、12. 下列条件中,不能判定两个三角形全等的是( )A、有一个锐角相等和一组边相等的直角三角形 B、底边和底边上高线对应相等的等腰三角形 C、顶角和底边相等的等腰三角形 D、一条直角边和一条斜边对应相等的直角三角形
A、 B、 C、 D、12. 下列条件中,不能判定两个三角形全等的是( )A、有一个锐角相等和一组边相等的直角三角形 B、底边和底边上高线对应相等的等腰三角形 C、顶角和底边相等的等腰三角形 D、一条直角边和一条斜边对应相等的直角三角形二、解答题(共12题,共84分)
-
13. 如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:

⑴涂黑部分的面积是原正方形面积的一半;
⑵涂黑部分成轴对称图形.
如图乙是一种涂法,请在图1~3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙)
14. 图①和图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的长均为1.请分别画出符合要求的图形,所画图形的各顶点必须与方格纸中的小正方形的顶点重合.
 (1)、请在图①中出一个面积为3的等腰三角形;(2)、请在图②中画出一个与△ABC全等的三角形ABD .
(1)、请在图①中出一个面积为3的等腰三角形;(2)、请在图②中画出一个与△ABC全等的三角形ABD .
15. 已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=50°,AB=AC,AD=AE,连结BD、CE,BD所在直线交CE、AC分别于点F、G. (1)、求证:△BAD≌△CAE;(2)、求∠BFC的度数.16. 如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
(1)、求证:△BAD≌△CAE;(2)、求∠BFC的度数.16. 如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求: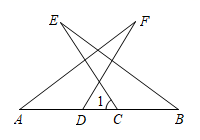 (1)、∠1的度数;
(1)、∠1的度数;
(2)、AC的长.
17. 已知:点O到△ABC的两边AB、AC所在直线的距离OE、OF相等,且OB=OC.(1)、如图,若点O在边BC上,求证:AB=AC; (2)、如图,若点O在△ABC的内部,则(1)中的结论还成立吗?若成立,请证明;若不成立,说明理由;
(2)、如图,若点O在△ABC的内部,则(1)中的结论还成立吗?若成立,请证明;若不成立,说明理由; (3)、若点O在△ABC的外部,则(1)的结论还成立吗?请画图表示.18. 问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(3)、若点O在△ABC的外部,则(1)的结论还成立吗?请画图表示.18. 问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明); (1)、特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;(2)、归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为.19. 已知:如图,点D在△ABC的外部,点C在DE边上,BC与AD交于点O.∠1=∠2=∠3,AB=AD.求证:△ACE是等腰三角形.
(1)、特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;(2)、归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为.19. 已知:如图,点D在△ABC的外部,点C在DE边上,BC与AD交于点O.∠1=∠2=∠3,AB=AD.求证:△ACE是等腰三角形.
证明:∵∠1=∠3( ),
∴∠1+∠CAD=∠3+∠CAD,
即∠BAC=∠_▲_.
∵∠1=∠2,
∠▲_=∠COD,
∴180°﹣∠1﹣∠AOB=180°﹣∠2﹣∠COD,
即∠B=∠D.
又∵AB=AD,
∴△ABC≌△ADE( ),
∴AC=AE( ),
∴△ACE是等腰三角形( ).
20. 已知:如图1,线段AD=5,点B从点A出发沿射线AD方向运动,以AB为底作等腰△ABC,使得AC=BC=AB. (1)、如图2,当AB=10时,求证:CD⊥AB;(2)、当△BCD是以BC为腰的等腰三角形时,求BC的长;(3)、当AB>5时,在线段BC上是否存在点E,使得△BDE与△ACD全等,若存在,求出BC的长;若不存在,请说明理由;(4)、作点A关于直线 CD的对称点A′,连结 CA′当CA′∥AB时,求CA′=(请直接写出答案).21. 【问题情境】
(1)、如图2,当AB=10时,求证:CD⊥AB;(2)、当△BCD是以BC为腰的等腰三角形时,求BC的长;(3)、当AB>5时,在线段BC上是否存在点E,使得△BDE与△ACD全等,若存在,求出BC的长;若不存在,请说明理由;(4)、作点A关于直线 CD的对称点A′,连结 CA′当CA′∥AB时,求CA′=(请直接写出答案).21. 【问题情境】在等边△ABC的两边AB , AC上分别有两点M , N , 点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC .

【特例探究】
如图1,当DM=DN时,
(1)、∠MDB=度;(2)、MN与BM , NC之间的数量关系为;(3)、【归纳证明】如图2,当DM≠DN时,猜想MN与BM , NC之间的数量关系,并加以证明.
(4)、【拓展应用】△AMN的周长与△ABC的周长的比为 .
22. 已知:如图1,在等边三角形ABC的BC,AC边上各取一点P,Q,使BP=CQ,AP,BQ相交于点O.

 (1)、求证:△ABP≌△BCQ;(2)、求∠BOP的度数;(3)、如图2,沿AB将△ABC折叠得到△ABD连结OD交AB于点H,求∠BOD的度数;(4)、请你直接写出DO、AO、BO之间的数量关系.23. 如图1,已知直线l垂直线段AB于点B,点P是直线l上异于点B的一个动点,线段AP绕点P顺时针旋转 得到线段CP,线段BP绕点P逆时针旋转 得到线段DP,连结AC,BD,CD,CD与直线l交于点E, .
(1)、求证:△ABP≌△BCQ;(2)、求∠BOP的度数;(3)、如图2,沿AB将△ABC折叠得到△ABD连结OD交AB于点H,求∠BOD的度数;(4)、请你直接写出DO、AO、BO之间的数量关系.23. 如图1,已知直线l垂直线段AB于点B,点P是直线l上异于点B的一个动点,线段AP绕点P顺时针旋转 得到线段CP,线段BP绕点P逆时针旋转 得到线段DP,连结AC,BD,CD,CD与直线l交于点E, . (1)、如图2,过点C作直线l的垂线,垂足为F.
(1)、如图2,过点C作直线l的垂线,垂足为F.①求证: .
②求PE的长.
(2)、在点P的运动过程中,点P,E,B三点中,是否存在其中一点恰是另外两点为端点的线段的中点,若存在,求出相应CD的长.若不存在,说明相应理由.24. 问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明); (1)、特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;(2)、归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、拓展应用:如图④,在△ABC中,AB=AC,A B>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为.
(1)、特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;(2)、归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、拓展应用:如图④,在△ABC中,AB=AC,A B>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为.