2022-2023学年浙教版数学八上期中复习专题3 证明
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 用反证法证明命题:“如图,如果AB//CD,AB//EF,那么CD//EF.”证明的第一个步骤是( )
 A、假定CD//EF B、假定CD不平行于EF C、已知AB//EF D、假定AB不平行于EF2. 下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )A、
A、假定CD//EF B、假定CD不平行于EF C、已知AB//EF D、假定AB不平行于EF2. 下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )A、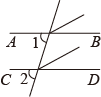 B、
B、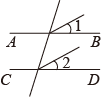 C、
C、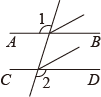 D、
D、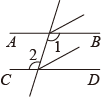 3. 定理:三角形的内角和等于 .
3. 定理:三角形的内角和等于 .已知:的三个内角为 , , .
求证: .
证法1
证法2
如图1,延长到点D,则(三角形的一个外角等于和它不相邻的两个内角的和).
∵(平角的定义),
∴(等量代换).

如图2,过点作 , ∵ ,
(两直线平行,内错角相等),
(两直线平行,内错角相等),
又∵(平角定义),
∴(等量代换).

下列说法正确的是( )
A、证法1采用了从特殊到一般的方法证明了该定理 B、证法1用合理的推理证明了该定理 C、证法2还需证明其他形状的三角形,该定理的证明过程才完整 D、证法2用严谨的推理证明了该定理4. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:证明:如图,∵ , ∴∠1=90°.
∵ , ∴∠2=90°,
∴∠1=∠2,∴ .
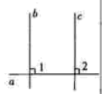
已知该证明过程是正确的,则证明的真命题是( )
A、在同一平面内,若 , 且 , 则 B、在同一平面内,若 , 且 , 则 C、同位角相等,两直线平行 D、两直线平行,同位角相等5. 课堂上,王老师要求学生设计图形来证明勾股定理,同学们经过讨论,给出两种图形,能证明勾股定理的是( ) A、①行,②不行 B、①不行,②行 C、①,②都行 D、①,②都不行6. 数学课上,老师出示了如下图的一道证明题.
A、①行,②不行 B、①不行,②行 C、①,②都行 D、①,②都不行6. 数学课上,老师出示了如下图的一道证明题.
其中①②③分别填写( )
A、中线、、一组对边平行且相等 B、中位线、、两组对边分别相等 C、中线、、两组对边分别相等 D、中位线、、一组对边平行且相等7. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、 B、
B、 C、
C、 D、
D、 8. 在证明命题“若 , 则”是假命题时,下列选项中所举反例错误的是( )A、 B、 C、 D、9. 已知:如图, , , 求证:∥ . 下面为嘉琪同学的证明过程:
8. 在证明命题“若 , 则”是假命题时,下列选项中所举反例错误的是( )A、 B、 C、 D、9. 已知:如图, , , 求证:∥ . 下面为嘉琪同学的证明过程:
证明:∵ , ( ① ),
∴ . 又∵ , ∴
∴∥( ② ).
其中①②为解题依据,则下列描述正确的是( )
A、①代表内错角相等 B、②代表同位角相等,两直线平行 C、①代表对顶角相等 D、②代表同旁内角相等,两直线平行10. 下列说法错误的是( )A、定义反映出事物的本质属性.既可以做性质,也可以做判定 B、证明两个等边三角形全等,具需证明一边相等即可 C、有一个角是 的等腰三角形是等腰直角三角形 D、在放大镜下,一个字可以变大,一条线段可以变长,但是一个角的大小是不变的二、解答题(共8题,共66分)
-
11. 如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.

证明:∵()
∴∠CDA=90°,∠DAB=90°().
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴(),
∴DF∥AE().
12. 完成下面的证明.已知:如图,∠1+∠2=180°,∠3+∠4=180°.
求证:AB∥EF .
证明:∵∠1+∠2=180°,
∴AB∥().
∵∠3+∠4=180°,
∴∥ .
∴AB∥EF().
 13. 【阅读】在证明命题“如果 , , 那么”时,小明的证明方法如下:
13. 【阅读】在证明命题“如果 , , 那么”时,小明的证明方法如下:证明:∵ ,
∴> ▲ . ∴ ▲ .
∵ , ,
∴ ▲ . ∴ ▲ .
∴.
【问题解决】
(1)、请将上面的证明过程填写完整;(2)、有以下几个条件:① , ② , ③ , ④ .请从中选择两个作为已知条件 , 得出结论 .你选择的条件序号是 ,并给出证明过程 .

