2022-2023学年浙教版数学八上期中复习专题1 认识三角形

试卷更新日期：2022-10-15 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. △ABC的三个内角∠A，∠B，∠C满足∠A：∠B：∠C＝3：4：5，则这个三角形是（）

A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形

查看试题解析
2. 下列命题中是假命题的是（）

A、一个三角形中至少有两个锐角 B、在同一平面内，过一点有且只有一条直线与已知直线垂直 C、同角的余角相等 D、一个角的补角大于这个角本身

查看试题解析
3. 画△ABC的边BC上的高，下列画法正确的是（）

A、 B、 C、 D、

查看试题解析
4. 在 $△ A B C$ 中，线段AP，AQ，AR分别是BC边上的高线，中线和角平分线，则（）

A、 $A P \leq A Q$ B、 $A Q \leq A R$ C、 $A P > A R$ D、 $A P > A Q$

查看试题解析
5. 如图，给你一张锐角三角形纸片，请你用折叠的方式，折出过点 $A$ 的角平分线、中线、高线，能成功折出的是（）

A、角平分线 B、中线 C、高线 D、都可以

查看试题解析
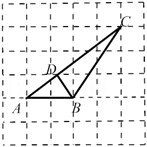
6. 如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG⊥CE于点G，CD＝AE.若BD＝6，CD＝5，则△DCG的面积是（）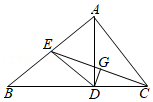

A、10 B、5 C、 $\frac{10}{3}$ D、 $\frac{5}{3}$

查看试题解析
7. 下列命题是假命题的是（）

A、等底等高的两个三角形面积相等 B、两个全等三角形的面积相等 C、面积相等的两个三角形全等 D、等腰三角形底边上的高线和中线互相重合

查看试题解析
8. 已知线段a＝2cm，b＝4cm，则下列长度的线段中，能与a，b组成三角形的是（）

A、8cm B、6cm C、4cm D、2cm

查看试题解析
9. 在△ABC中，有下列条件：不能确定△ABC是直角三角形的条件是（）

A、∠A+∠B=∠C； B、∠A：∠B：∠C=1：2：3； C、∠A=2∠B=3∠C； D、∠A=∠B=∠

查看试题解析
10. 如图，为了估计一池塘岸边两点A，B之间的距离，小颖同学在池塘一侧选取了一点P，测得PA＝100m，PB＝90m，那么点A与点B之间的距离可能是（）

A、10m B、120m C、190m D、220m

查看试题解析

二、解答题（共8题，共66分）

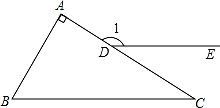
11. 如图，在△ABC中，∠ACB=114°，∠B=46°，CD平分∠ACB，CE为AB边上的高，求∠DCE的度数.

查看试题解析
12. 如图，已知△ABC ，请按下列要求作图：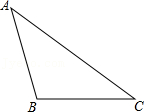

⑴用直尺和圆规作△ABC的角平分线CG ．

⑵作BC边上的高线．

查看试题解析
13. 小王准备用一段长30m的篱笆围成一个三角形形状的场地，用于饲养家兔，已知第一条边长为am，由于受地势限制，第二条边长只能是第一条边长的2倍多2m.

(1)、请用a表示第三条边长.

(2)、问第一条边长可以为7m吗？请说明理由.

查看试题解析
14. 在Rt△ABC中，∠ACB＝90°，∠A＝40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E.

(1)、求∠CBE的度数；

(2)、过点D作DF//BE，交AC的延长线于点F，求∠F的度数.

查看试题解析
15. 如图，在 $Δ A B C$ 中， $A E$ 是边 $B C$ 上的高线.

(1)、若 $A D$ 是 $B C$ 边上的中线， $A E = 3 cm$ ， $S_{Δ A B C} = 12 {cm}^{2}$ .求 $D C$ 的长.

(2)、若 $A D$ 是 $∠ B A C$ 的平分线， $∠ B = 40 °$ ， $∠ C = 50 °$ ，求 $∠ D A E$ 的大小.

查看试题解析
16. 如图1，AD平分∠BAC，AE⊥BC，∠B=30°，∠C=70°。

(1)、∠BAC=°， ∠DAE=°；

(2)、如图2，若把“AE⊥BC"变成“点F在AD的延长线上，FE⊥BC“，其它条件不变，求∠DFE的度数；

(3)、如图3，AD平分∠BAC，AE平分∠BEC，∠C-∠B=40°，求∠DAE的度数。

查看试题解析
17. 如图，在 $Δ A B C$ 中， $∠ C = 60 °$ ， $A D$ 是高线，两条角平分线 $A E$ 和 $B F$ 交于点 $O$ .

(1)、求 $∠ E O F$ 的度数.

(2)、若 $∠ A B C = α$ 度（ $α > 60 °$ ），用含 $α$ 的代数式表示 $∠ E A D$ 的度数.

查看试题解析
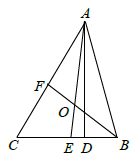18.

(1)、如图①，AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系？为什么？

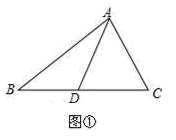(2)、若三角形的面积记为S，例如：△ABC的面积记为S_△_ABC.如图②，已知S_△_ABC＝1.△ABC的中线AD、CE相交于点O，求四边形BDOE的面积.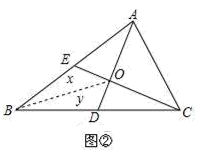

小华利用(1)的结论，解决了上述问题，解法如下：
连接BO，设S_△_BEO＝x，S_△_BDO＝y，由(1)结论可得：S_△_BCE＝S_△_BAD＝ $\frac{1}{2}$ S_△_ABC＝ $\frac{1}{2}$ ，S_△_BCO＝2S_△_BDO＝2y，S_△_BAO＝2S_△_BEO＝2x.则有 ${\begin{array}{l} S_{△ B E O} + S_{△ B C O} = S_{△ B C E} \\ S_{△ B A O} + S_{A B D O} = S_{△ B A D} \end{array}$ 即 ${\begin{array}{l} x + 2 y = \frac{1}{2} \\ 2 x + y = \frac{1}{2} \end{array}$ 所以x＋y＝ $\frac{1}{3}$ .即四边形BDOE面积为 $\frac{1}{3}$ .
请仿照上面的方法，解决下列问题：
Ⅰ.如图③，已知S△ABC＝1.D、E是BC边上的三等分点，F、G是AB边上的三等分点，AD、CF交于点O，求四边形BDOF的面积.
Ⅱ.如图④，已知S_△_ABC＝1.D、E、F是BC边上的四等分点，G、H、I是AB边上的四等分点，AD、CG交于点O，则四边形BDOG的面积为.

查看试题解析

三、填空题（每题4分，共24分）

19. 如图，在△ABC中，AB=AC，CD是高线，E是AC的中点，若AB=4，则DE= ．

查看试题解析
20. 如图，△ABC的三个顶点均在小方格的格点上，BD⊥AC于点D.若每个小方格的边长为1，则BD的长为 .

查看试题解析
21. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ A - ∠ B = 30 °$ ，则 $∠ A =$ ．

查看试题解析
22. 如图所示，在△ABC中，∠A＝90°，点D在AC边上，DE∥BC.若∠1＝156°，则∠B＝度.

查看试题解析
23. 如图，在△ABC中，AB＝AC，AD是BC边上的高，点E、F是AD的三等分点，若BC＝4cm，AD＝6cm，则图中阴影部分的面积是cm².

查看试题解析
24. 若等腰三角形的两边长分别为1和5，则该等腰三角形的周长为．

查看试题解析