（人教版）2022-2023学年度第一学期九年级数学 因式分解法 期中复习

试卷更新日期：2022-10-15 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 方程(x+1)2=3(x+1)的根为（　　　）
    A、2 B、x1=2 ， x2=−1 C、x1=3 ， x2=−1 D、x=−1

    查看试题解析

  • 2. 若关于x的一元二次方程(m−1)x2+5x+m2−3m+2=0有一个根为0，则m的值为（    ）
    A、0 B、1或2 C、1 D、2

    查看试题解析

  • 3. 已知直角三角形有两条边长分别是方程x2﹣14x+48＝0的两个根，则该直角三角形的斜边长是（    ）
    A、10 B、27 C、10或8 D、10或27

    查看试题解析

  • 4. 一元二次方程 x2=x 的解为（   ）
    A、−x=1 B、x1=x2=1 C、x1=0 ， x2=1 D、x1=x2=0

    查看试题解析

  • 5. 方程﹣x（x+1）＝0的解是（　　）
    A、x＝﹣1 B、x1＝﹣1，x2＝0 C、x＝0 D、x1＝1，x2＝0

    查看试题解析

  • 6. 一个等腰三角形的两条边长分别是方程x2−7x+10=0的两根，则该等腰三角形的周长是（  ）
    A、12 B、11 C、9 D、16

    查看试题解析

  • 7. 一元二次方程x2－3x＝0的根是（   ）
    A、x＝0 B、x＝3 C、x1＝0，x2＝3 D、x1＝0，x2＝－3

    查看试题解析

  • 8. 若x2﹣3x的值等于零，则x的值为（   ）
    A、﹣3 B、0 C、0或3 D、0或﹣3

    查看试题解析

  • 9. 三角形两边的长分别是8和6，第三边的长是方程x2-12x+20=0的一个实数根，则此三角形的周长是（ ）
    A、24 B、24或16 C、16 D、22

    查看试题解析

  • 10. 已知三角形的两边长为2和5，第三边满足方程x2−7x+12=0 ， 则三角形的周长为（       ）
    A、10 B、11 C、10或11 D、以上都不对

    查看试题解析

二、填空题

三、解答题

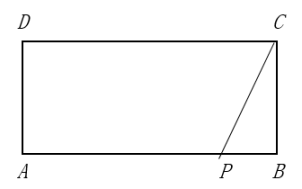
  • 16. 先化简，再求值：(2x−1−1x)÷x2−1x2−2x+1 ， 其中x是方程x2-3x+2=0的解． 

    查看试题解析

  • 17. 矩形ABCD中，AB=17，BC=21 ， 点P在AB边上，且满足AP=3PC，求PB之长．

    查看试题解析

  • 18. 已知关于x的方程x2−6x+m2−3m−5=0的一个根为一1，求另一个根及m的值.

    查看试题解析

  • 19. 阅读下面的例题：解方程 x2−|x|−2=0

    解：当x≥0时，原方程化为x2－x－2＝0，解得：x1＝2，x2＝－1（不合题意，舍去）；

    当x＜0时，原方程化为x2＋ x－2＝0，解得：x1＝1，（不合题意，舍去）x2＝－2；

    ∴原方程的根是x1＝2，x2＝－2.

    请参照例题解方程 x2−|x−1|−1=0 .

    查看试题解析

  • 20. 若a≠0且a2-2a=0，求方程16x2-4ax+1=3-12x的根。

    查看试题解析

  • 21. 已知关于x的方程mx2﹣（m+2）x+2＝0（m≠0），若方程的两个实数根都是整数，求正整数m的值．

    查看试题解析

  • 22. 如图，平行四边形ABCD中，AE⊥BC于E，AE＝EB＝EC＝a，且a是一元二次方程x2+2x﹣3＝0的根，求平行四边形ABCD的周长．

    查看试题解析

  • 23. 阅读理解下列材料然后回答问题：

    解方程：x²-3|x|+2=0

    解：（1）当x≥0时，原方程化为x²-3x+2=0，解得： x1 =2， x2 =1

    （ 2 ）当x＜0时，原方程化为x²+3x+2=0，解得： x1 =1， x2 =-2.

    ∴原方程的根是 x1 =2， x2 =1， x3 =1， x4 =-2.

    请观察上述方程的求解过程，试解方程x²-2|x-1|-1=0.

    查看试题解析