2022-2023学年浙教版数学七上期中复习专题8 实数及其运算

试卷更新日期：2022-10-15 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 在实数5 $\frac{2}{5}$ ，﹣ $\sqrt{4}$ ， $0. \overset{\cdot}{7} 1 \overset{\cdot}{2}$ ， $\sqrt{8}$ ， $\frac{π}{2}$ ，1.12112111211112…（每两个2之间依次多一个1）中，无理数有（）个.

A、2 B、3 C、4 D、5

查看试题解析
2. 实数 $\frac{1}{3}$ ， $\frac{\sqrt{2}}{4}$ ， $\frac{π}{6}$ 中，分数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 下列说法错误的是（）

A、 $\sqrt{81}$ 的平方根是 $\pm 3$ B、 ${(- 1)}^{2012}$ 是最小的正整数 C、两个无理数的和一定是无理数 D、实数与数轴上的点——对应

查看试题解析
4. 下列说法：
①一个数的平方根等于它本身，这个数是0或1；②实数包括无理数和有理数；③2的算术平方根是 $\sqrt{2}$ ；④无理数是带根号的数．正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列说法中：①0是最小的的整数；②有理数不是正数就是负数；③正整数、负整数、正分数、负分数统称为有理数；④非负数就是正数；⑤ $- \frac{π}{2}$ 是有理数；⑥平方等于它本身的数有±1；⑦无限小数都不是有理数；⑧正数中没有最小的数，负数中没有最大的数.其中错误的说法的个数为（）

A、7个 B、6个 C、5个 D、4个

查看试题解析
6. 如图，若数轴上的点A，B，C，D表示数﹣1，1，2，3，则表示数 $4 - \sqrt{11}$ 的点应在（）

A、A，O之间 B、B，C之间 C、C，D之间 D、O，B之间

查看试题解析
7. 如图，数轴上C，B两点表示的数分别是2， $\sqrt{13}$ ，且点C是AB的中点，则点A表示的数是（）

A、 $\sqrt{13}$ ﹣4 B、3﹣ $\sqrt{13}$ C、4﹣ $\sqrt{13}$ D、 $\sqrt{13}$ ﹣3

查看试题解析
8. 已知 $a ， b ， c$ 三个数，a为8- $\sqrt{8}$ ， b为7- $\sqrt{7}$ ， c为6- $\sqrt{6}$ ，则这三个数的大小关系是（）

A、 $c < b < a$ B、 $b < c < a$ C、 $a = b = c$ D、 $b < a < c$

查看试题解析
9. 估计30的算术平方根位于哪两个整数之间（）

A、2与3 B、3与4 C、4与5 D、5与6

查看试题解析
10. 面积为11的正方形的边长为x，则（）

A、2<x<3 B、3<x<4 C、4<x<5 D、5<x<6

查看试题解析

二、填空题（每空2分，共18分）

11. 有下列四种说法：
①数轴上有无数多个表示无理数的点；

②带根号的数不一定是无理数；

③没有最大的负实数，但有最小的正实数；

④没有最大的正整数，但有最小的正整数.

其中说法错误的有 (注：填写出所有错误说法的编号)。

查看试题解析
12. 比较大小： $- \frac{3}{4}$ $- \frac{4}{5}$ ， 4 $\sqrt{13}$ （填“＞、＜、＝”）.

查看试题解析
13. 若 $\sqrt{7}$ 的整数部分为a，小数部分为b，则b= ，数轴上表示实数a，b的两点之间距离为。

查看试题解析
14. 如图，以数轴的单位长度线段为边长作一个正方形，以表示数2的点为圆心，正方形对角线长为半径画半圆，交数轴于点A和点B，则点A表示的数是．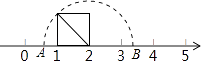

查看试题解析
15. 规定：用符号[x]表示一个不大于实数x的最大整数，例如：[3.69]＝3，[ $\sqrt{3}$ +1]＝2，[﹣2.56]＝﹣3，[﹣ $\sqrt{3}$ ]＝﹣2.按这个规定，[﹣ $\sqrt{13}$ ﹣1]＝.

查看试题解析
16. 任何实数a，可用[a]表示不大于a的最大整数，如[4]＝4，[ $\sqrt{3}$ ]＝1，现对72进行如下操作：72 $\underset{\to}{第一次}$ [ $\sqrt{72}$ ]＝8 $\underset{\to}{第二次}$ ＝[ $\sqrt{8}$ ]＝2 $\underset{\to}{第三次}$ [ $\sqrt{2}$ ]＝1，这样对72只需进行3次操作后变为1.类似地：

(1)、对83只需进行次操作后变为1；

(2)、只需进行3次操作后变为1的所有正整数中，最大的数是 .

查看试题解析

三、计算题（每题8分，共16分）

17. 计算：

(1)、﹣10+5﹣3

(2)、 $| - \frac{1}{2} | \times 8 - {(- 2)}^{2} \times \frac{1}{4}$

(3)、 $（ - 1 ）^{2021} + 2^{3} \times \sqrt{\frac{1}{16}} - \sqrt[3]{- 27}$

(4)、 $- 3^{2} - 6 \div (- 3) \times \sqrt[3]{64}$

查看试题解析
18. 计算.

(1)、﹣5﹣（﹣6）× $\frac{1}{6}$ .

(2)、4.8﹣（﹣1.2）+（﹣6）+|﹣4|.

(3)、 $3 \times (- \frac{4}{5}) \div \frac{9}{10}$ .

(4)、 $\sqrt[3]{- 8} - \sqrt{1 - \frac{16}{25}} + | 2 - \sqrt{5} | + \sqrt{(- 4)^{2}}$ .

查看试题解析

四、解答题（共8题，共46分）

19. 把下列各数之前的序号填在相应的大括号内：
① $\frac{2}{3}$ ，②−0.31，③−（−2），④ $- \sqrt[3]{27}$ ，⑤ $\sqrt{3}$ ，⑥0，⑦ $\frac{π}{3}$ ，⑧1.1010010001…（每两个1之间依次多一个0），⑨1.732

(1)、正分数集合：{}

(2)、负有理数集合：{}

(3)、无理数集合：{}

(4)、非负整数集合：{}

查看试题解析
20. 在数轴上表示下列各数，并把这些数按从小到大的顺序进行排列，用“＜”连接：
π，4，－1.5，0， $\sqrt{3}$ ，－ $\sqrt{2}$ .

查看试题解析
21. 如图，已知实数 $- \sqrt{5}$ ，－1， $\sqrt{5}$ ，4，其在数轴上所对应的点分别为点A，B，C，D．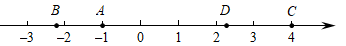

(1)、点B表示的数为，点D表示的数为；

(2)、点C与点D之间的距离为；

(3)、记点A与点B之间距离为a，点C与点D之间距离为b，求a+b的值．

查看试题解析
22. 如图，每个小正方形的边长均为1可以得到每个小正方形的面积为1.

(1)、请在图中的 $5 \times 5$ 的方格内作出边长为 $\sqrt{13}$ 的正方形；

(2)、请在数轴上表示出 $- 1 + \sqrt{13}$ .

查看试题解析
23. 某高速公路规定汽车的行驶速度不得超过100千米/时，当发生交通事故时，交通警察通常根据刹车后车轮滑过的距离估计车辆的行驶速度，所用的经验公式是v＝16 $\sqrt{d f}$ ，其中v表示车速（单位：千米/时，d表示刹车后车轮滑过的距离（单位：米），f表示摩擦系数.在一次交通事故中，经测量d＝32米，f＝2，请你判断一下，肇事汽车当时是否超速了.

查看试题解析
24.

(1)、用“＜”“＞”“=”填空: $\sqrt{1}$ $\sqrt{2}$ $\sqrt{3}$

(2)、由上可知: ① $| \sqrt{1} - \sqrt{2} | =$ 。
② $| \sqrt{2} - \sqrt{3} |$ =。

(3)、计算:(结果保留根号)
$| \sqrt{1} - \sqrt{2} | + | \sqrt{2} - \sqrt{3} | + | \sqrt{3} - \sqrt{4} | + | \sqrt{4} - \sqrt{5} | + \dots + | \sqrt{2010} - \sqrt{2011} |$ .

查看试题解析
25. 如图，是一个数值转换器，原理如图所示．

(1)、当输入的x值为16时，求输出的y值；

(2)、是否存在输入的x值后，始终输不出y值？如果存在，请直接写出所有满足要求的x值；如果不存在，请说明理由．

(3)、输入一个两位数x，恰好经过两次取算术平方根才能输出无理数，则x= ．

查看试题解析
26. 阅读下面文字，然后回答问题．
给出定义：一个实数的整数部分是不大于这个数的最大数，这个实数的小数部分为这个数与它的整数部分的差的绝对值．例如：2.4的整数部分为2，小数部分为 $2.4 - 2 = 0.4$ ； $\sqrt{2}$ 的整数部分为1，小数部分可用 $\sqrt{2} - 1$ 表示；再如，﹣2.6的整数部分为﹣3，小数部分为 $| - 2.6 - (- 3) | = 0.4$ ．由此我们得到一个真命题：如果 $\sqrt{2} = x + y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，那么 $x = 1$ ， $y = \sqrt{2} - 1$ ．

(1)、如果 $\sqrt{7} = a + b$ ，其中 $a$ 是整数，且 $0 < b < 1$ ，那么 $a =$ ， $b =$ ；

(2)、如果 $- \sqrt{7} = c + d$ ，其中 $c$ 是整数，且 $0 < d < 1$ ，那么 $c =$ ， $d =$ ；

(3)、已知 $3 + \sqrt{7} = m + n$ ，其中m是整数，且 $0 < n < 1$ ，求 $| m - n |$ 的值；

查看试题解析