（人教版）2022-2023学年度第一学期八年级数学等腰三角形期中复习

试卷更新日期：2022-10-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，已知 $A C$ 平分 $∠ D A B$ ， $C E ⊥ A B$ 于 $E$ ， $A B = A D + 2 B E$ ，则下列结论： $① A B + A D = 2 A E$ ； $② ∠ D A B + ∠ D C B = 180 °$ ； $③ C D = C B$ ； $④ S_{△ A C E} - 2 S_{△ B C E} = S_{△ A D C}$ ；其中正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ A = 40 °$ ，观察图中尺规作图的痕迹，可知 $∠ B C G$ 的度数为（）

A、40° B、50° C、55° D、60°

查看试题解析
3. 如图，在△ABC中，AB=AC，∠A=36°，以B为圆心，BC的长为半径圆弧，交AC于点D，连接BD，则∠ABD等于（ )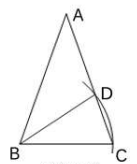

A、36° B、46° C、54° D、72°

查看试题解析
4. 如图，已知直角三角形ABC中，∠ACB=90°，∠CAB=60°，在直线BC或AC上取一点P，使得△ABP为等腰三角形，则符合条件的点有（）

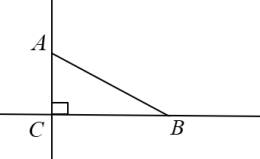A、4个 B、5个 C、6个 D、7个

查看试题解析
5. 等腰三角形的两边分别为7和4，则它的周长是（）

A、 $15$ B、 $18$ C、 $15 或 18$ D、 $11$

查看试题解析
6. 如图，△ABC与△BDE是全等的等边三角形，且A、B、D三点共线，AE、CD交于点O，∠AEB＝∠EAB．现有如下结论：①∠AED＝90°；②∠BCD+∠AEB＝60°，③OB⊥AD；④AE＝CD；⑤OB平分∠CBE，平分∠AOD；⑥AO+OB＝AD；一定成立的有（）个．

A、5个 B、6个 C、3个 D、4个

查看试题解析
7. 如图， $∠ A O B = 30 °$ ，点P在 $∠ A O B$ 的内部，点C，D分别是点P关于 $O A$ 、 $O B$ 的对称点，连接 $C D$ 交 $O A$ 、 $O B$ 分别于点E、F；若 $△ P E F$ 的周长的为10，则线段 $O P =$ （）．

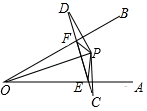A、8 B、9 C、10 D、11

查看试题解析
8. 如图，△ABC中，∠C＝90°，AB＝8，∠B＝30°，点P是BC边上的动点，则AP长不可能是（）

A、3.5 B、4.2 C、5.8 D、7.3

查看试题解析
9. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $A C = 4$ ，则 $A B$ 的长是（）

A、8 B、1 C、2 D、4

查看试题解析
10. 如图，某社会实践学习小组为测量学校A与河对岸江景房B之间的距离，在学校附近选一点C，利用测量仪器测得 $∠ A = 60 °$ ， $∠ C = 90 °$ ， AC=300米．由此可求得学校与江景房之间的距离 $A B$ 等于 $($ 　　 $)$

A、150米 B、600米 C、800米 D、1200米

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 和 $△ D B C$ 中， $∠ A = 40 °$ ， $A B = A C = 4$ ， $∠ B D C = 140 °$ ， $B D = C D$ ，以点 $D$ 为顶点作 $∠ M D N = 70 °$ ，两边分别交 $A B$ ， $A C$ 于点 $M$ ， $N$ ，连接 $M N$ ，则 $△ A M N$ 的周长为．

查看试题解析
12. 如图，在 $R t △ A B F$ 中， $∠ A F B = 90 °$ ， $△ C D E$ 的顶点 $E$ 在 $△ A B F$ 的边 $B F$ 上，点 $C$ 在 $B F$ 的延长线上， $∠ C = ∠ B$ ，且 $C D = C E$ ，若 $∠ A = 36 °$ ，则 $∠ D$ 的度数为．

查看试题解析
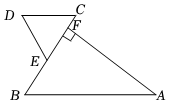13. 如图，在△ABC中，∠ABC＝∠ACB，D为BC的中点，连接AD，E是AB上的一点，P是AD上一点，连接EP、BP，AC=10，BC=12，则EP+BP的最小值是.

查看试题解析
14. 如图， $∠ B A C = 30 °$ ， $A M$ 是 $∠ B A C$ 的平分线，过 $M$ 作 $M E / / B A$ 交 $A C$ 于 $E$ ，作 $M D ⊥ B A$ ，垂足为 $D$ ， $M E = 10 c m$ ，则 $M D =$ ．

查看试题解析
15. 如图，在△ABC中，∠ACB=90°，∠B =30°，CD是高．若AD=2，则BD= ．

查看试题解析

三、解答题

16. 如图， $△ A B C$ 与 $△ D C B$ 中，AC与BD交于点E，且 $∠ A = ∠ D$ ， $A B = D C$ ，求证： $∠ E B C = ∠ E C B$ ．

查看试题解析
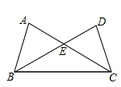17. 如图，在等腰三角形ABC中，AB=AC，点D为AC上一点，且AD=BD=BC，则∠A等于多少？

查看试题解析
18. 已知：如图，在 $△ A B C$ 中， $A B = A C$ ，D是BC的中点， $D E ⊥ A B$ ， $D F ⊥ A C$ ，E ， F是垂足， $A E = A F$ 吗？请说明理由．

查看试题解析
19. 已知：如图，∠EAC是△ABC的一个外角.请从①AB＝AC，②AD平分∠EAC，③AD∥BC中任选两个当条件，第三个当结论构成一个命题.如果该命题是真命题，请你证明；如果该命题是假命题，请说明理由.

查看试题解析
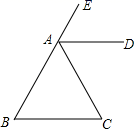20. 如图，在△ABC中， $A B = A C$ ， D、E是△ABC内的两点，AD平分∠BAC， $∠ E B C = ∠ E = 60 °$ ．若 $B E = 6 c m$ ， $D E = 2 c m$ ，求BC的长．

查看试题解析
21. 如图，△ABC是等边三角形，D、E在边AB、AC的延长线上，且DE $∥$ BC，分别交AB，AC于点D，E.求证：△ADE是等边三角形.

查看试题解析
22. 已知：如图，在△ABC中，∠ACB＝90°，∠A＝30°．求证：BC＝ $\frac{1}{2}$ AB．

查看试题解析
23. 如图，△ABC是等边三角形，BD平分∠ABC交AC于点D，过点D作 $E F ⊥ A B$ 于E，交BC边延长线于F，若 $A E = 2$ ，求BF的长．

查看试题解析

（人教版）2022-2023学年度第一学期八年级数学 等腰三角形 期中复习

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年度第一学期八年级数学等腰三角形期中复习