(人教版)2022-2023学年度第一学期八年级数学 角的平分线的性质 期中复习
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题
-
1. 如图, , 平分交于点 , , , , 分别是 , 延长线上的点,和的平分线交于点下列结论:;;平分;为定值其中结论正确的有( )
 A、1个 B、2个 C、3个 D、4个2. 如图,ABC中,AD平分∠BAC,AB=4,AC=2,若ACD的面积等于3,则ABD的面积为( )
A、1个 B、2个 C、3个 D、4个2. 如图,ABC中,AD平分∠BAC,AB=4,AC=2,若ACD的面积等于3,则ABD的面积为( )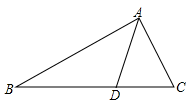 A、 B、4 C、6 D、123. 如图,在△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,BC=8cm,BD:CD=3:4,则点D到AC的距离为( )cm.
A、 B、4 C、6 D、123. 如图,在△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,BC=8cm,BD:CD=3:4,则点D到AC的距离为( )cm. A、3 B、4 C、 D、4. 如图,在Rt△ABC中,∠C=90˚,AD平分∠BAC , 交BC于点D , AB=10,S△ABD=25,则CD的长为( )
A、3 B、4 C、 D、4. 如图,在Rt△ABC中,∠C=90˚,AD平分∠BAC , 交BC于点D , AB=10,S△ABD=25,则CD的长为( ) A、2.5 B、4 C、5 D、105. 如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )
A、2.5 B、4 C、5 D、105. 如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB;④S△PAC=S△MAP+S△NCP .
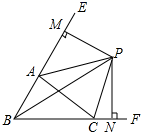 A、1个 B、2个 C、3个 D、4个6. 如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=( )
A、1个 B、2个 C、3个 D、4个6. 如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=( ) A、3cm B、7.5cm C、6cm D、4.5cm7. 如图,AD是的角平分线,于 , 已知的面积为28. , , 则AB的长为( )
A、3cm B、7.5cm C、6cm D、4.5cm7. 如图,AD是的角平分线,于 , 已知的面积为28. , , 则AB的长为( ) A、4 B、6 C、8 D、108. 如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于 EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法错误的是( )
A、4 B、6 C、8 D、108. 如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于 EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法错误的是( ) A、∠ADB=∠ABC B、AB=BD C、AC=AD+BD D、∠ABD=∠BCD9. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB , 若CD=10,则点D到AB的距离是( )
A、∠ADB=∠ABC B、AB=BD C、AC=AD+BD D、∠ABD=∠BCD9. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB , 若CD=10,则点D到AB的距离是( )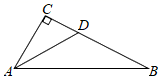 A、8 B、9 C、10 D、1110. 如图,在 中, 平分 交 于点D , ,若点P是 上的动点,则线段 的最小值是( )
A、8 B、9 C、10 D、1110. 如图,在 中, 平分 交 于点D , ,若点P是 上的动点,则线段 的最小值是( ) A、2.4 B、3 C、4 D、5
A、2.4 B、3 C、4 D、5二、填空题
-
11. 如图,在平面直角坐标系中,将△OAB沿x轴向右平移后得到△O'A'B',点A的坐标为(0,4),点A的对应点A在直线y x﹣1上,点B在∠A'AO的角平分线上,若四边形AA'B'B的面积为4,则点B的坐标为 .
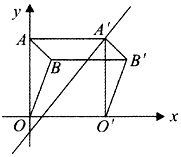 12. 如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
12. 如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .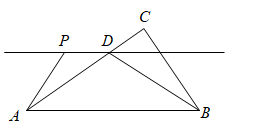 13. 如图:在中, , 以顶点C为圆心,适当长为半径画弧,分别交、于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点D,若 , , 则的面积为.
13. 如图:在中, , 以顶点C为圆心,适当长为半径画弧,分别交、于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点D,若 , , 则的面积为.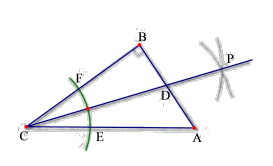 14. 在RtABC中,∠C=90°,若BC=6,AD平分∠BAC交BC于点D,BD=2CD,则点D到线段AB的距离为 .
14. 在RtABC中,∠C=90°,若BC=6,AD平分∠BAC交BC于点D,BD=2CD,则点D到线段AB的距离为 .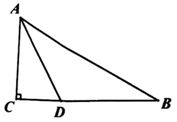 15. 如图,在△ABC中,∠C=90°,AD平分∠BAC , AB=5,CD=2,则△ABD的面积是 .
15. 如图,在△ABC中,∠C=90°,AD平分∠BAC , AB=5,CD=2,则△ABD的面积是 .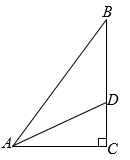
三、解答题
-
16. 如图:在 , , 于 , 于 , 、相交于求证:平分 .
 17. 已知:如图,PC平分∠APB,CM⊥PA于M,CN⊥PB于N,D、E分别是边PA和PB上的点,且CD=CE.求证:∠APB+∠DCE=180°.
17. 已知:如图,PC平分∠APB,CM⊥PA于M,CN⊥PB于N,D、E分别是边PA和PB上的点,且CD=CE.求证:∠APB+∠DCE=180°.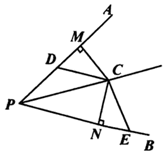 18. 如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB,求证:AD=CD+AB.
18. 如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB,求证:AD=CD+AB. 19. 如图,AB=AC,BD=DC,DF⊥AB,DE⊥AC,垂足分别是F,E.求证:DE=DF.
19. 如图,AB=AC,BD=DC,DF⊥AB,DE⊥AC,垂足分别是F,E.求证:DE=DF. 20. 如图,点P是∠AOB的角平分线OC上一点,PE⊥OA,OE=12cm,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4cm,求△PGE的面积.
20. 如图,点P是∠AOB的角平分线OC上一点,PE⊥OA,OE=12cm,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4cm,求△PGE的面积.


