(人教版)2022-2023学年度第一学期八年级数学 全等三角形的判定 期中复习
试卷更新日期:2022-10-15 类型:复习试卷
一、单选题
-
1. 如图, , 且 , 则判定≌的最好理由是( )
 A、 B、 C、 D、2. 如图所示 , 要说明≌ , 需添加的条件不能是( )
A、 B、 C、 D、2. 如图所示 , 要说明≌ , 需添加的条件不能是( ) A、 B、 C、 D、3. 在△ABC中,AC=6,中线AD=10,则AB边的取值范围是( )A、16<AB<22 B、14<AB<26 C、16<AB<26 D、14<AB<224. 如图所示,、、分别表示的三边长,则下面与一定全等的三角形是( )
A、 B、 C、 D、3. 在△ABC中,AC=6,中线AD=10,则AB边的取值范围是( )A、16<AB<22 B、14<AB<26 C、16<AB<26 D、14<AB<224. 如图所示,、、分别表示的三边长,则下面与一定全等的三角形是( )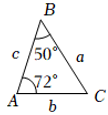 A、
A、 B、
B、 C、
C、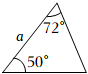 D、
D、 5. 如图用直尺和圆规作已知角的平分线的示意图,由≌可得 , 由作图的过程可知,说明≌的依据是( )
5. 如图用直尺和圆规作已知角的平分线的示意图,由≌可得 , 由作图的过程可知,说明≌的依据是( ) A、 B、 C、 D、6. 如图, , , 欲证≌ , 则补充的条件中不正确的是( )
A、 B、 C、 D、6. 如图, , , 欲证≌ , 则补充的条件中不正确的是( )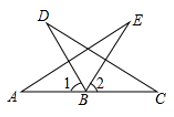 A、 B、 C、 D、7. 如图,是的中线,交的延长于点 , , , 则的取值可能是( )
A、 B、 C、 D、7. 如图,是的中线,交的延长于点 , , , 则的取值可能是( ) A、3 B、6 C、8 D、128. 如图, , 添加下列条件,不能使≌的是( )
A、3 B、6 C、8 D、128. 如图, , 添加下列条件,不能使≌的是( ) A、 B、 C、 D、9. 如图,已知 , , 不能判定≌的是( )
A、 B、 C、 D、9. 如图,已知 , , 不能判定≌的是( )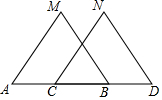 A、 B、 C、 D、10. 如图,已知 , 要得到≌ , 还需要从下列条件中补选一个,补上仍不能判断其全等的是( )
A、 B、 C、 D、10. 如图,已知 , 要得到≌ , 还需要从下列条件中补选一个,补上仍不能判断其全等的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知,如图, , , 那么图中共有对全等三角形.
 12. 如图所示 , , , , 则
12. 如图所示 , , , , 则 13. 已知,如图, , , 那么图中≌ .
13. 已知,如图, , , 那么图中≌ . 14. 如图,PA=PB,请你添加一个适当的条件: , 使得△PAD≌△PBC.
14. 如图,PA=PB,请你添加一个适当的条件: , 使得△PAD≌△PBC.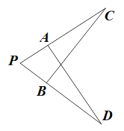 15. 如图,线段AB,CD相交于点O,AO=BO,添加一个条件, 能使 , 所添加的条件的是 .
15. 如图,线段AB,CD相交于点O,AO=BO,添加一个条件, 能使 , 所添加的条件的是 .
三、解答题
-
16. 已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
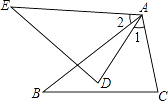 17. 如图, , , , 图中 , 有怎样的数量关系和位置关系?试证明你的结论.
17. 如图, , , , 图中 , 有怎样的数量关系和位置关系?试证明你的结论. 18. 如图,是的高,是上一点,交于 , 且有 , , 试说明 .
18. 如图,是的高,是上一点,交于 , 且有 , , 试说明 . 19. 如图, 是 的中线,F为 上一点,E为 延长线上一点,且 .求证: .
19. 如图, 是 的中线,F为 上一点,E为 延长线上一点,且 .求证: . 20. 如图,在ABC和CDE中,点B、D、C在同一直线上,已知∠ACB=∠E,AC=CE,ABDE,求证:ABC≌CDE.
20. 如图,在ABC和CDE中,点B、D、C在同一直线上,已知∠ACB=∠E,AC=CE,ABDE,求证:ABC≌CDE. 21. 如图,在△ABC中,AB=AC,点D在AB上,点E在AC上,AD=AE.求证:CD=BE.
21. 如图,在△ABC中,AB=AC,点D在AB上,点E在AC上,AD=AE.求证:CD=BE. 22. 如图,已知: , , . 求证: .
22. 如图,已知: , , . 求证: . 23. 【实际问题】在拓展训练过程中,小明和组员为了完成测河宽的任务,在不能过河测量又没有任何测量工具的情况下,设计出下面的方案:小明面向河对岸的方向站好,然后调整帽子,使视线通过帽檐正好落在河对岸一点;然后,他转过身,保持刚才的姿态,这时视线通过帽檐落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是河的宽度.
23. 【实际问题】在拓展训练过程中,小明和组员为了完成测河宽的任务,在不能过河测量又没有任何测量工具的情况下,设计出下面的方案:小明面向河对岸的方向站好,然后调整帽子,使视线通过帽檐正好落在河对岸一点;然后,他转过身,保持刚才的姿态,这时视线通过帽檐落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是河的宽度.
【数学建模】将小明看成一条线段 , 河对岸一点为点 , 自己所在岸的那个点为点 , 示意图如图所示,请你根据示意图帮助小明同学将问题补充完整,并解释其中的道理.
如图,如果于点 , ▲ ,那么 .
【问题解决】说明AC=AD的理由.
