江苏省南京市六校2022-2023学年高一上学期数学10月联考试卷

试卷更新日期：2022-10-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 设全集 $U = {- 2 ， - 1 ， 0 ， 1 ， 2 ， 3}$ ，集合 $A = {- 1 ， 0 ， 1}$ ， $B = {- 1 ， 2 ， 3}$ ，则 $A ∩ ∁_{U} B$ $=$ （）

A、{-1} B、 ${0 ， 1}$ C、 ${2 ， 3}$ D、 ${1 ， 2 ， 3}$

查看试题解析
2. 已知 $a \in R$ ，则 $a > 2$ 是 $a^{2} > 2 a$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 下列各式中成立的一项是（）

A、 ${(\frac{a}{b})}^{3} = a^{3} b^{\frac{1}{3}}$ B、 $\sqrt[12]{{(- 2)}^{4}} = \sqrt[3]{- 2}$ C、 $\sqrt{\sqrt[3]{4}} = \sqrt[3]{2}$ D、 $\sqrt[4]{a^{3} - b^{3}} = {(a - b)}^{\frac{3}{4}}$

查看试题解析
4. 设实数 $x$ 满足 $x > 1$ ，函数 $y = 2 + 3 x + \frac{4}{x - 1}$ 的最小值为（）

A、 $4 \sqrt{2} + 1$ B、6 C、 $4 \sqrt{3} - 1$ D、 $4 \sqrt{3} + 5$

查看试题解析
5. 十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“＝”作为等号使用，后来英国数学家哈利奥特首次使用“＜”和“＞”符号，并逐渐被数学界接受，不等号的引入对不等式的发展影响深远．下列说法正确的是（）

A、若a<b，c<d，则ac<bd B、若a＜b，则 $\frac{1}{a + 1}$ ＞ $\frac{1}{b + 1}$ C、若 $\frac{a^{2}}{b}$ ＞ $\frac{a^{2}}{c}$ ，则 $\frac{1}{b} > \frac{1}{c}$ D、若a＞b，c＞d，则 $\frac{a + c}{b + c}$ ＞ $\frac{a + d}{b + d}$

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分对应值见下表：
x
－2
－1
0
1
3
y
－12
－6
－2
0
－2
则下列结论正确的是（）

A、 $a > 0$ B、该二次函数的零点为1 C、关于 $x$ 的不等式 $a x^{2} + b x + c < 0$ 的解集为 $(1 ， 2)$ D、 $a - b + c < 0$

查看试题解析
7. 已知命题“ $\exists x \in R ， (m + 1) x^{2} + (m + 1) x + 1 \leq 0$ ”是真命题，则实数 $m$ 的取值范围是（）

A、 $(- \infty ， - 1) ∪ [3 ， + \infty)$ B、 $[- 1 ， 3]$ C、 $(- 1 ， 3)$ D、 $(- \infty ， 0] ∪ [1 ， + \infty)$

查看试题解析
8. 用C(A)表示非空集合A中的元素个数，定义 $A * B = {\begin{array}{l} C (A) - C (B) ， C (A) \geq C (B) \\ C (B) - C (A) ， C (A) < C (B) \end{array}$ .若 $A = {0 ， 1}$ ， $B = {x | x (x + a) \cdot (x^{2} + a x + 1) = 0}$ ，且 $A * B = 1$ ，设实数a的所有可能取值组成的集合是S，则C(S)等于（）

A、1 B、3 C、5 D、7

查看试题解析

二、多选题

9. 设非空集合 $P$ ， $Q$ 满足 $P ∩ Q = P$ ，且 $P \neq Q$ ，则下列选项中正确的是（）

A、 $\forall x \in Q$ ，有 $x \in P$ B、 $\exists x \in Q$ ，使得 $x \notin P$ C、 $\exists x \in P$ ，使得 $x \notin Q$ D、 $\forall x \notin Q$ ，有 $x \notin P$

查看试题解析
10. 下列说法错误的是（）

A、 $a x^{2} > 0 (a > 0)$ 的解集为 $R$ B、不等式 $x^{2} + x + 1 < 0$ 的解集为 $\emptyset$ C、如果 $a x^{2} + b x + c = 0$ 中 $a < 0$ ， $Δ = 0$ ，则 $a x^{2} + b x + c \geq 0$ 的解集是 ${x | x \neq - \frac{b}{2 a}}$ D、 $x^{2} + 3 x - 4 > 0$ 的解集和不等式组 ${\begin{array}{l} x - 1 > 0 \\ x + 4 > 0 \end{array}$ 的解集相同

查看试题解析
11. 已知a＞0，b＞0，且a＋b＝4，则（）

A、 $a b \leq 4$ B、 $a^{2} + b^{2} \leq 8$ C、 $\frac{1}{a} + \frac{1}{b} \geq 1$ D、 $\sqrt{a} + \sqrt{b} \leq 2 \sqrt{2}$

查看试题解析
12. 已知 $p ： | 2 x - 1 | < 3$ ， $q ： 2 x^{2} - a x - a^{2} \leq 0$ ，若 $p$ 是 $q$ 的一个必要不充分条件，则实数 $a$ 的取值范围可以是（）

A、 $(- 1 ， 0)$ B、 $(- 2 ， 0]$ C、 $(- 1 ， 1)$ D、 $(- 1 ， 2]$

查看试题解析

三、填空题

13. 命题“ $\forall x \in Q$ ， $x^{2} - 2 > x$ ”的否定为．

查看试题解析
14. 已知 $a ＞ 0 ， b ＞ 0$ ，化简： $(\sqrt[3]{a})^{3} \cdot \sqrt{a b^{3}}$ = ．（用分数指数幂表示）

查看试题解析
15. 已知全集 $U = R$ ， $N = {x | x^{2} + 2 x < 0}$ ， $M = {x | \frac{x + 1}{x^{2} + 1} < 0}$ ，则图中阴影部分表示的集合是．

查看试题解析
16. “勾股容方”问题出自我国汉代数学名著《九章算术》，该问题可以被描述为：“设一直角三角形(如图1)的两直角边长分别为a和b，求与该直角三角形具有公共直角的内接正方形的边长”，公元263年，数学家刘徽为《九章算术》作注，在注中他利用出入相补原理给出了上述问题如图2和图3所示的解答，则图1中与直角三角形具有公共直角的内接正方形的边长为，当内接正方形的面积为1时，则图3中两个标有“朱”的三角形和两个标有“青”的三角形的面积总和的最小值为.

查看试题解析

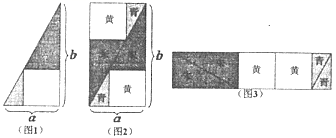
四、解答题

17.

(1)、求值： ${(\frac{1}{100})}^{- \frac{1}{2}} - \sqrt{{(1 - \sqrt{2})}^{2}} - 8 \times {(\sqrt{2} - \sqrt{3})}^{0} - 2 7^{\frac{1}{3}}$

(2)、已知非零实数a满足 $a - a^{- 1} = 2$ ，求 $\frac{(a + a^{- 1}) (a^{2} + a^{- 2} + 6)}{(a^{2} - a^{- 2})}$ 的值.

查看试题解析
18. 已知 $p$ ：关于 $x$ 的方程 $x^{2} - a x + a^{2} - a - 5 = 0$ 有实数根， $q ： m - 1 \leq a \leq m + 3$ ．

(1)、若命题 $p$ 是真命题，求实数 $a$ 的取值范围；

(2)、若 $q$ 是 $p$ 的充分不必要条件，求实数 $m$ 的取值范围．

查看试题解析
19. 在① $A ∩ B \neq \emptyset$ ， ② $A ∩ B = B$ ， ③ $B \subseteq ∁_{R} A$ 这三个条件中任选一个，补充在下面问题中，并完成解答.
问题：已知集合 $A = {x | (x - a - 3) (x - a) < 0 ， x \in R}$ ， $B = {x | \frac{2}{x + 1} > 1 ， x \in R}$ ，是否存在实数 $a$ ，使得_________，若实数 $a$ 存在，求 $a$ 的取值范围；若不存在，说明理由.

查看试题解析
20. 甲、乙两同学探讨了一个问题：已知正实数 $x ， y$ 满足 $3 x + y = 1$ ，求 $\frac{1}{x} + \frac{1}{y}$ 的最小值.

(1)、甲给出的解法：由 $1 = 3 x + y \geq 2 \sqrt{3 x \cdot y}$ ，得 $\sqrt{x y} \leq \frac{\sqrt{3}}{6}$ ，所以 $\frac{1}{x} + \frac{1}{y} \geq 2 \sqrt{\frac{1}{x} \cdot \frac{1}{y}} = 2 \sqrt{\frac{1}{x y}} \geq 4 \sqrt{3}$ .所以 $\frac{1}{x} + \frac{1}{y}$ 的最小值为 $4 \sqrt{3}$ .而乙却说甲的解法是错的，请你指出其中的问题，并给出正确的解法；

(2)、结合上述问题探讨，试求函数 $y = \frac{1}{x} + \frac{1}{1 - 2 x} (0 < x < \frac{1}{2})$ 的最小值.

查看试题解析
21. 建国70年来，我们始终坚持保护环境和节约资源，坚持推进生态文明建设.市政府也越来越重视生态系统的重建和维护，若市财政下拨一项专款100百万元，分别用于植绿护绿和处理污染两个生态维护项目，植绿护绿项目五年内带来的生态收益M $($ 单位：百万元 $)$ 与投放资金 $x ($ 单位：百万元 $)$ 的函数关系为： $M = 0.25 x$ ，处理污染项目五年内带来的生态收益 $N ($ 单位：百万元 $)$ 与投放资金 $x ($ 单位：百万元 $)$ 的函数关系为： $N = \frac{40 x + 64}{x + 8}$ ．生态项目的投资开始利润薄弱，只有持之以恒，才能功在当代，利在千秋.试问：如何对两个项目进行资金分配，才能使两个生态项目五年内带来的收益总和最大，收益总和最大值是多少？

查看试题解析
22. 设函数 $y = a x^{2} + (1 - a) x + a + 2$ ．

(1)、若函数有两个负的零点，求实数 $a$ 的取值范围；

(2)、若当 $x \in (0 ， 2]$ 时，函数 $y = a x^{2} + (1 - a) x + a + 2$ 图象恒在函数 $y = 3 x^{2} - (a + 1) x + a + 3$ 图象的下方，求实数 $a$ 的取值范围.

查看试题解析

x	－2	－1	0	1	3
y	－12	－6	－2	0	－2