辽宁省沈阳市重点高中联合体2022-2023学年高三上学期数学9月月考试卷

试卷更新日期：2022-10-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图，已知集合 $U = R$ ，集合 $A = {1 ， 2 ， 3 ， 4 ， 5}$ ， $B = {x | (x + 1) (x - 2) \leq 0}$ ，则图中阴影部分表示的集合的子集的个数为（）

A、3 B、4 C、7 D、8

查看试题解析
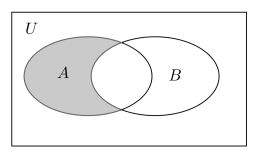2. “幂函数 $f (x) = (m^{2} + m - 1) x^{m}$ 在 $(0 ， + ∞)$ 上为增函数”是“函数 $g (x) = 2^{x} - m^{2} \cdot 2^{- x}$ 为奇函数”的（）条件

A、充分不必要 B、必要不充分 C、充分必要 D、既不充分也不必要

查看试题解析
3. 中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初步健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其大意为：“有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地．”则该人最后一天走的路程为（）

A、6里 B、5里 C、4里 D、3里

查看试题解析
4. 设 $a = \frac{1}{2} c o s 6 ° - \frac{\sqrt{3}}{2} s i n 6 ° ， b = \frac{2 t a n 13 °}{1 - t a n^{2} 13 °} ， c = \sqrt{\frac{1 - c o s 50 °}{2}} ，$ 则有（）

A、 $a > b > c$ B、 $a < b < c$ C、 $a < c < b$ D、 $b < c < a$

查看试题解析
5. 已知 $a > 0$ ， $b > 0$ ， $a b = 1$ ，则 $\frac{a^{2} + b^{2} + 6}{a + b}$ 的最小值为（）

A、2 B、4 C、 $2 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
6. 已知 $c o s (\frac{5}{2} π - α) = 2 c o s (2 π + α)$ ，且 $t a n (α + β) = \frac{1}{3}$ ，则 $t a n β$ 的值为（）

A、-7 B、7 C、1 D、-1

查看试题解析
7. 已知偶函数 $f (x)$ 的定义域为 $R$ ，且当 $x \geq 0$ 时， $f (x) = \frac{x - 1}{x + 1}$ ，则使不等式 $f (a^{2} - 2 a) < \frac{1}{2}$ 成立的实数 $a$ 的取值范围是（）

A、 $(- 1 ， 3)$ B、 $(- 3 ， 3)$ C、 $(- 1 ， 1)$ D、 $(- \infty ， 3)$

查看试题解析
8. 已知函数 $f (x) = \frac{l n x}{x}$ ， $g (x) = l n (x + 1) + 2 a x^{2}$ ，若 $∀ x_{1} \in [1 ， e^{2}]$ ， $\exists x_{2} \in (0 ， 1)$ 使得 $f (x_{1}) > g (x_{2})$ 成立，则实数a的取值范围是（）

A、 $(- \infty ， - \frac{l n 2}{2})$ B、 $(- \infty ， - \frac{l n 2}{2}]$ C、 $(- \infty ， - \frac{1}{e})$ D、 $(- \infty ， e - \frac{l n 2}{2}]$

查看试题解析

二、多选题

9. 下列结论正确的是（）

A、“ $x > \sqrt{5}$ ”是“ $x^{2} > 5$ ”的充分不必要条件 B、 $\frac{t a n \frac{π}{8}}{1 + t a n^{2} \frac{π}{8}} = \frac{1}{2}$ C、已知在前 $n$ 项和为 $S_{n}$ 的等差数列 ${a_{n}}$ 中，若 $a_{7} = 5$ ，则 $S_{13} = 65$ D、已知 $a > 0 ， b > 0 ， a + b = 1$ ，则 $\frac{1}{a} + \frac{4 - b}{b}$ 的最小值为 $8$

查看试题解析
10. 下列选项中，正确的是（）

A、函数 $f (x) = a^{x - 1} - 2$ （ $a > 0$ 且 $a \neq 1$ ）的图象恒过定点 $(1 ， - 2)$ B、若不等式 $a x^{2} + b x + 3 > 0$ 的解集为 ${x | - 1 < x < 3}$ ，则 $a + b = 2$ C、若 $p ： \exists n \in N$ ， $n^{2} > 2^{n}$ ，则 $\neg p ： \forall n \in N$ ， $n^{2} \leq 2^{n}$ D、函数 $f (x) = l n x + x - 2$ 恰有1个零点．

查看试题解析
11. 已知 $0 < θ < \frac{π}{4}$ ，若 $s i n 2 θ = m$ ， $c o s 2 θ = n$ 且 $m \neq n$ ，则下列选项中与 $t a n (\frac{π}{4} - θ)$ 恒相等的有（）

A、 $\frac{n}{1 + m}$ B、 $\frac{m}{1 + n}$ C、 $\frac{1 - n}{m}$ D、 $\frac{1 - m}{n}$

查看试题解析
12. 已知 $f (x)$ 是定义在R上的偶函数，且 $f (x + 3) = f (x - 1)$ ，若当 $x \in [0 ， 2]$ 时， $f (x) = 2^{x} - 1$ ，则下列结论正确的是（）

A、当 $x \in [- 2 ， 0]$ 时， $f (x) = 2^{- x} - 1$ B、 $f (2019) = 7$ C、 $y = f (x)$ 的图象关于点（2，0）对称 D、函数 $g (x) = f (x) - l o g_{2} x$ 有3个零点

查看试题解析

三、填空题

13. 在等差数列 ${a_{n}}$ 中， $a_{1} < a_{2}$ ， $a_{7} a_{11} = 6$ ， $a_{4} + a_{14} = 5$ ，则该数列公差 $d =$ ．

查看试题解析
14. 已知 $s i n (α + \frac{π}{4}) = \frac{3}{5}$ ，则 $s i n 2 α =$ .

查看试题解析
15. 已知方程x²＋3ax＋3a＋1＝0（a>1）的两根分别为tan α，tan β，且α，β∈ $(- \frac{π}{2} ， \frac{π}{2})$ ，则α＋β＝.

查看试题解析
16. 定义在 $R$ 上函数 $f (x)$ 满足 $f (x + 1) = \frac{1}{2} f (x)$ ，且当 $x \in [0 ， 1)$ 时， $f (x) = 1 - | 2 x - 1 |$ ．若对任意 $x \in [m ， + \infty)$ ，都有 $f (x) \leq \frac{3}{64}$ ，则 $m$ 的取值范围是．

查看试题解析

四、解答题

17.

(1)、计算： $\frac{c o s 1 0^{∘} - \sqrt{3} c o s 10 0^{∘}}{\sqrt{1 - c o s 8 0^{∘}}}$ ；

(2)、已知 $s i n α = - 2 c o s α$ ，求 $\frac{s i n (\frac{π}{2} + α) - 3 s i n (π + α)}{2 c o s (\frac{3 π}{2} - α) - c o s (π - α)}$ 的值.

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中，顶点在坐标原点，以 $x$ 轴非负半轴为始边的锐角 $α$ 与钝角 $β$ 的终边与单位圆O分别交于A，B两点， $x$ 轴的非负半轴与单位圆O交于点M，已知 $S_{△ O A M} = \frac{\sqrt{5}}{5} ，$ 点B的横坐标是 $- \frac{7 \sqrt{2}}{10}$ .

(1)、求 $c o s (α - β)$ 的值；

(2)、求 $2 α - β$ 的值.

查看试题解析
19. 从条件① $2 S_{n} = (n + 1) a_{n} ， a_{n} > 0$ ；② ${a_{n}}^{2} + a_{n} = 2 S_{n} ， a_{n} > 0$ ；③ $\sqrt{S_{n}} + \sqrt{S_{n - 1}} = a_{n} (n \geq 2)$ 中任选一个，补充在下面问题中，并给出解答.
已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 1$ ， ____.

(1)、求 ${a_{n}}$ 的通项公式；

(2)、 $[x]$ 表示不超过 $x$ 的最大整数，记 $b_{n} = [l g a_{n}]$ ，求 ${b_{n}}$ 的前100项和 $T_{100}$ .

查看试题解析
20. 已知函数 $f (x) = a e^{x} - x$

(1)、若 $a = 1$ ，求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、讨论函数 $f (x)$ 的单调性；

(3)、设 $g (x) = f (x) - x^{2} + x + 3$ ，若函数 $g (x)$ 有两个零点，求 $a$ 的取值范围.

查看试题解析
21. 定义在R上的函数f（x）满足：如果对任意的x₁ ， x₂∈R，都有f（ $\frac{x_{1} + x_{2}}{2}$ ） $\leq \frac{f (x_{1}) + f (x_{2})}{2}$ ，则称函数f（x）是R上的凹函数，已知二次函数f（x）＝ax²+x（a∈R，a≠0）

(1)、当a＝1，x∈[﹣2，2]时，求函数f（x）的值域；

(2)、当a＝1时，试判断函数f（x）是否为凹函数，并说明理由；

(3)、如果函数f（x）对任意的x∈[0，1]时，都有|f（x）|≤1，试求实数a的范围．

查看试题解析
22. 已知函数 $f (x) = \frac{l n x + a}{x} ， a \in R$ ．

(1)、若 $x = 1$ 是 $f (x)$ 的极值点，求a；

(2)、当 $a \leq - 1$ 时，证明： $f (x) \leq e^{x - 2} - 1$ ．

查看试题解析