2022年秋季北师版数学九年级上册第四章 《图形的相似》单元检测B
试卷更新日期:2022-10-14 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )A、1 :3 B、1:6 C、1:9 D、3:12. 如图,在△ABC中,D,E分别是AB和AC上的点,DE∥BC,若= , 那么=( )
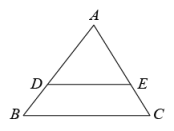 A、 B、 C、 D、3. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( )
A、 B、 C、 D、3. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( ) A、2 B、 C、 D、4. 如图,在中,是边上的点, , , 则与的周长比是( )
A、2 B、 C、 D、4. 如图,在中,是边上的点, , , 则与的周长比是( ) A、 B、 C、 D、5. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、 B、 C、 D、5. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )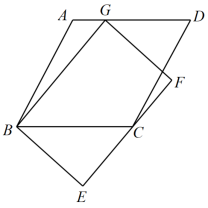 A、 B、 C、 D、36. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( )
A、 B、 C、 D、36. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( ) A、 B、 C、10 D、7. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( )
A、 B、 C、10 D、7. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( ) A、9 B、12 C、15 D、188. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )
A、9 B、12 C、15 D、188. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )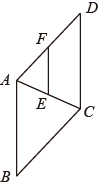 A、11 B、22 C、33 D、449. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、11 B、22 C、33 D、449. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、810. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、2 B、4 C、6 D、810. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每题3分,共18分)
-
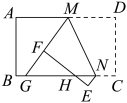
11. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
 12. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .
12. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .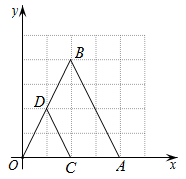 13. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).
13. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).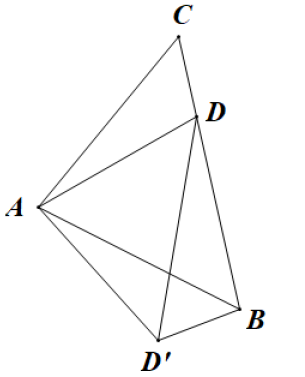 14. 如图,在矩形ABCD中,AB=6cm,BC=9cm,点E,F分别在边AB,BC上,AE=2cm,BD,EF交于点G,若G是EF的中点,则BG的长为cm.
14. 如图,在矩形ABCD中,AB=6cm,BC=9cm,点E,F分别在边AB,BC上,AE=2cm,BD,EF交于点G,若G是EF的中点,则BG的长为cm.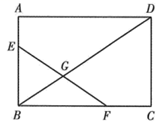 15. 如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若 = ,则 =.
15. 如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若 = ,则 =.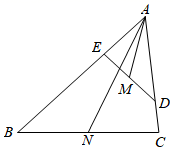 16. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=.
16. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=.
三、解答题(共8题,共72分)
-
17. 如图,在菱形中,点M,N分别是边 , 上的点, , . 连接 , , 延长交线段延长线于点E.
 (1)、求证:;(2)、若AD=4,则ME的长是 .18. 如图,在 中,点E、F分别在边 、 上,且 .
(1)、求证:;(2)、若AD=4,则ME的长是 .18. 如图,在 中,点E、F分别在边 、 上,且 .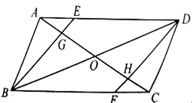 (1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.19. 如图,在 中,D在 上, , .
(1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.19. 如图,在 中,D在 上, , . (1)、求证: ∽ ;(2)、若 ,求 的值.20. 如图,在正方形ABCD中,点E,F分别为边BC,CD上的点,且AE⊥BF于点P,G为AD的中点,连接GP,过点P作PH⊥GP交AB于点H,连接GH.
(1)、求证: ∽ ;(2)、若 ,求 的值.20. 如图,在正方形ABCD中,点E,F分别为边BC,CD上的点,且AE⊥BF于点P,G为AD的中点,连接GP,过点P作PH⊥GP交AB于点H,连接GH. (1)、求证:BE=CF;(2)、若AB=6,BE BC,求GH的长.21. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.
(1)、求证:BE=CF;(2)、若AB=6,BE BC,求GH的长.21. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.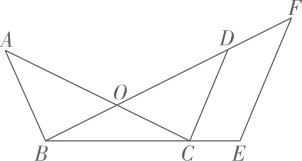 (1)、求证 ;(2)、若 ,求 的长.22. 如图,在平行四边形中,是一条对角线,且 , , , 是边上两点,点在点的右侧, , 连接 , 的延长线与的延长线相交于点 .
(1)、求证 ;(2)、若 ,求 的长.22. 如图,在平行四边形中,是一条对角线,且 , , , 是边上两点,点在点的右侧, , 连接 , 的延长线与的延长线相交于点 .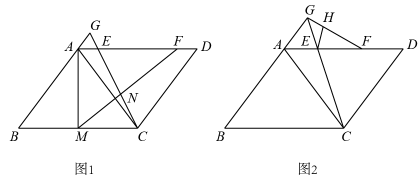 (1)、如图1,是边上一点,连接 , , 与相交于点 .
(1)、如图1,是边上一点,连接 , , 与相交于点 .①若 , 求的长;
②在满足①的条件下,若 , 求证:;
(2)、如图2,连接 , 是上一点,连接 . 若 , 且 , 求的长.23. 已知在 ABC中,O为BC边的中点,连接AO,将 AOC绕点O顺时针方向旋转(旋转角为钝角),得到 EOF,连接AE,CF.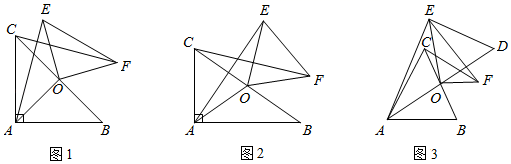 (1)、如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)、如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.24. 如图,
(1)、如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)、如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.24. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).